Question

5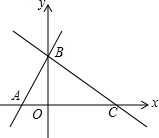．如图，一次函数y=（m-1）x+4的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB面积为4．
（1）求m的值及点A的坐标．
（2）过点B作直线BC与x轴的正半轴相交于点C，且OC=3OA，求直线BC的函数表达式．

Answer 1

分析 （1）先求得OB=4，然后根据三角形面积求得OA的长，即可求得A的坐标，把A的坐标代入y=（m-1）x+4，即可求得m的值；
（2）根据OC=3OA得出C的坐标，然后直线BC的函数表达式为y=kx+b，代入C（6，0）、B（0，4），根据待定系数法即可求得．

解答 解：（1）由一次函数y=（m-1）x+4可知点B（0，4），
∴OB=4，
∵S_△OAB=4，
∴$\frac{1}{2}$×OA×OB=4，
∴OA=2，
∴A（-2，0），
把点A（-2，0）代入y=（m-1）x+4，得-2（m-1）+4=0，
解得m=3；
（2）∵OC=3OA，
∴OC=6，
∴点C的坐标为（6，0），
设直线BC的函数表达式为y=kx+b，代入C（6，0）、B（0，4），
得$\left\{\begin{array}{l}6k+b=0\\ b=4\end{array}$，解得k=-$\frac{2}{3}$，b=4，
∴直线BC的函数表达式为y=-$\frac{2}{3}$x+4．

点评 本题考查了两直线相交的问题，主要利用了待定系数法求一次函数解析式，三角形的面积，得到点B的坐标是解题的关键．