题目内容
 如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )
如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )| A、高 | B、中线 |
| C、角平分线 | D、不能确定 |
考点:三角形的面积
专题:
分析:过A作AE⊥BC,分别计算S△ACD、S△ABD,根据S△ACD=S△ABD即可求得BD=DC,即可解题.
解答:解:过A作AE⊥BC,

则S△ACD=
BD•AE,
S△ABD=
BC•AE,
∵S△ACD=S△ABD,
∴BD=BC,
∴AD为中线.
故选B.

则S△ACD=
| 1 |
| 2 |
S△ABD=
| 1 |
| 2 |
∵S△ACD=S△ABD,
∴BD=BC,
∴AD为中线.
故选B.
点评:本题考查了三角形面积的计算,考查了三角形中线的定义.本题中求证BD=DC是解题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、有两角和其中一角的对边对应相等的两个三角形全等 |
| B、全等三角形对应的角平分线相等 |
| C、斜边和一个锐角分别相等的两个直角三角形全等 |
| D、在△ABC和△A′B′C′中,若AB=BC=CA,A′B′=B′C′=C′A′,则△ABC≌△A′B′C′ |
 如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5
如图,在?ABCD中,BC=2CD,点M、N分别在BC、CD边上,AM与BN交于点E.若∠C=∠AEN,BN=5 如图,双曲线y=
如图,双曲线y=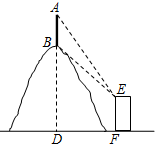 如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)
如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号) 如图,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都为1.顺次连接五个圆心得到五边形ABCDE,则图中五个阴影部分的面积之和是
如图,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都为1.顺次连接五个圆心得到五边形ABCDE,则图中五个阴影部分的面积之和是