题目内容
若α、β是一元二次方程x2+2x-6=0的两根,则α2+β2= .
考点:根与系数的关系
专题:
分析:利用根与系数的关系可得出α+β和αβ,且α2+β2=(α+β)2-2αβ,代入计算即可.
解答:解:
∵α、β是一元二次方程x2+2x-6=0的两根,
∴α+β=-2,αβ=-6,
∴α2+β2=(α+β)2-2αβ=(-2)2-2×(-6)=4+12=16,
故答案为:16.
∵α、β是一元二次方程x2+2x-6=0的两根,
∴α+β=-2,αβ=-6,
∴α2+β2=(α+β)2-2αβ=(-2)2-2×(-6)=4+12=16,
故答案为:16.
点评:本题主要考查一元二次方程根与系数的关系,把α2+β2化成(α+β)2-2αβ是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )
如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )| A、高 | B、中线 |
| C、角平分线 | D、不能确定 |
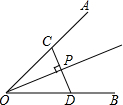 如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.
如图,P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于CD,则CD( )P点到∠AOB两边距离之和.| A、小于 | B、大于 |
| C、等于 | D、不能确定 |
代数式a=
,4xy,
,a,2014,
a2b,-
中,单项式的个数有( )
| 1 |
| 2a |
| a+b |
| 3 |
| 1 |
| 2 |
| 3mn |
| 4 |
| A、3个 | B、4个 | C、5个 | D、6个 |
已知m、n互为相反数,c、d互为倒数,则代数式5(m+n)-2cd的值为( )
| A、3 | B、-2 | C、-3 | D、0 |
若x,y均为非负数,则方程2012x=-2013y的解的情况是( )
| A、无解 | B、有唯一解 |
| C、有无数解 | D、不能确定 |
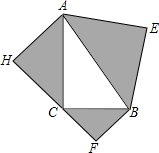 如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为