题目内容
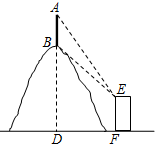 如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)
如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点E作EG⊥AD于点G;在Rt△BEG中,易知∠BEG=45°,得BG=EG;进而可在Rt△AGE中求得AG的大小,根据BD=BG+GD即可得答案.
解答: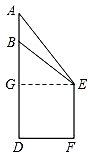 解:如图,过点E作EG⊥AD于点G.
解:如图,过点E作EG⊥AD于点G.
由已知得:∠AEG=60°,∠BEG=45°.
在Rt△BEG中,BG=EG.
在Rt△AEG中,由tan∠AEG=
,得AG=
EG=
BG.
∵AG=AB+BG=20+BG.
∴
BG=20+BG.
即BG=
=10(
+1).
∵BD=BG+GD,GD=EF=35.
∴BD=10(
+1)+35≈27.32+35=62.32≈62.3(m).
答:小山BD的高约为62.3m.
 解:如图,过点E作EG⊥AD于点G.
解:如图,过点E作EG⊥AD于点G.由已知得:∠AEG=60°,∠BEG=45°.
在Rt△BEG中,BG=EG.
在Rt△AEG中,由tan∠AEG=
| AG |
| EG |
| 3 |
| 3 |
∵AG=AB+BG=20+BG.
∴
| 3 |
即BG=
| 20 | ||
|
| 3 |
∵BD=BG+GD,GD=EF=35.
∴BD=10(
| 3 |
答:小山BD的高约为62.3m.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知一次函数y=kx-3,已知当x=-5时,y=7,那么k的值是( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
我们知道:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)= .(其中n为自然数).
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=
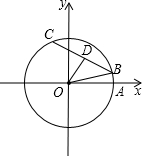 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )| A、22 | ||
| B、24 | ||
C、10
| ||
D、12
|
 如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )
如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )| A、高 | B、中线 |
| C、角平分线 | D、不能确定 |
代数式a=
,4xy,
,a,2014,
a2b,-
中,单项式的个数有( )
| 1 |
| 2a |
| a+b |
| 3 |
| 1 |
| 2 |
| 3mn |
| 4 |
| A、3个 | B、4个 | C、5个 | D、6个 |
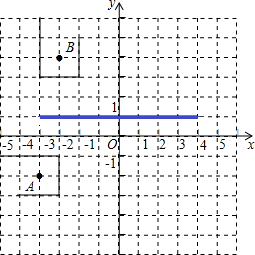 如图,机械手要将一个工件从图中的A处移动到B处,但是这个工件不能碰到图中的障碍(不包括坐标轴所表示的紫线),试用坐标写出一条机械手在移动中可能要经过的路线(机械手的行走路线均经过格点)
如图,机械手要将一个工件从图中的A处移动到B处,但是这个工件不能碰到图中的障碍(不包括坐标轴所表示的紫线),试用坐标写出一条机械手在移动中可能要经过的路线(机械手的行走路线均经过格点)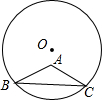 △ABC中,AB=AC=5,BC=8,半径为
△ABC中,AB=AC=5,BC=8,半径为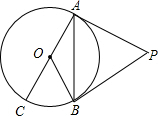 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.