题目内容
已知⊙O的直径AB为6cm,弦AC与AB的交角为30°,求弦BC的长及弦AC的弦心距.
考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:画出图形,求出∠ACB=90°,根据含30度角的直角三角形性质求出BC即可,求出OD是三角形ACB的中位线,得出OD=
BC,代入求出即可.
| 1 |
| 2 |
解答:解:如图,

∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6cm,∠CAB=30°,
∴BC=
AB=3cm;
∵OD为弦AC的弦心距,
∴OD⊥AC,
∵∠ACB=90°,
∴OD∥BC,
∵AO=BO,
∴AD=DC,
∴OD=
BC=1.5cm.

∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6cm,∠CAB=30°,
∴BC=
| 1 |
| 2 |
∵OD为弦AC的弦心距,
∴OD⊥AC,
∵∠ACB=90°,
∴OD∥BC,
∵AO=BO,
∴AD=DC,
∴OD=
| 1 |
| 2 |
点评:本题考查了圆周角定理,含30度角的直角三角形的性质,三角形的中位线的应用,解此题的关键是求出OD=
BC,BC=
AB.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
我们知道:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)= .(其中n为自然数).
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.根据前面各式规律,可以猜测:
1+3+5+7+9+…+(2n-1)=
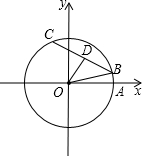 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )| A、22 | ||
| B、24 | ||
C、10
| ||
D、12
|
 如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )
如图,△ABC中,D为BC上的一点,且S△ACD=S△ABD,则AD为( )| A、高 | B、中线 |
| C、角平分线 | D、不能确定 |

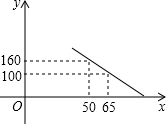 大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.
大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.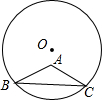 △ABC中,AB=AC=5,BC=8,半径为
△ABC中,AB=AC=5,BC=8,半径为