题目内容
7.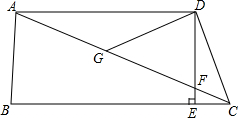 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.(1)说明DC=DG;
(2)若DG=7,EC=4,求DE的长.
分析 (1)根据直角三角形斜边上的中线的性质可得DG=AG,根据等腰三角形的性质可得∠GAD=∠GDA,根据三角形外角的性质可得∠CGD=2∠GAD,再根据平行线的性质和等量关系可得∠ACD=∠CGD,根据等腰三角形的性质可得CD=DG;
(2)根据勾股定理即可求解.
解答 (1)证明:∵DE⊥BC,
∴∠DEB=90°,
∵AD∥BC,
∴∠ADE+∠DEB=180°,
∴∠ADE=90°,
∵G为AF的中点,
∴DG=AG,
∴∠DAF=∠ADG,
∴∠DGC=∠DAF+∠ADG=2∠DAC,
∵AD∥BC,
∴∠ACB=∠DAC,
∵∠ACD=2∠ACB,
∴∠DGC=∠DCA,
∴DC=DG;
(2)解:∵在Rt△DEC中,∠DEC=90°,DG=DC=7,CE=4,
∴由勾股定理得:DE=$\sqrt{{7}^{2}-{4}^{2}}$=$\sqrt{33}$.
点评 本题考查了勾股定理,直角三角形斜边上中线性质,直角三角形的性质的应用,解此题的关键是求出DG=DC,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
17.已知a+b=2,则a2-b2+4b的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
12.已知二次函数y=-$\frac{1}{2}$x2-3x-$\frac{5}{2}$,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y2>y3>y1 | D. | y2<y3<y1 |

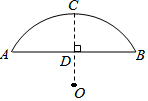 有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD,长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?
有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD,长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗? 已知BD为△ABC中线,CF∥BD,EF交BD于G,若BG=EG,BD=2,EF=3,求CF的长.
已知BD为△ABC中线,CF∥BD,EF交BD于G,若BG=EG,BD=2,EF=3,求CF的长.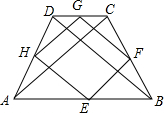 四边形ABCD中,DC∥AB,AC⊥BD,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.
四边形ABCD中,DC∥AB,AC⊥BD,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.