题目内容
14.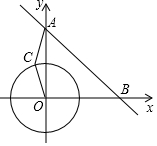 在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.
在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.(1)求直线AB的表达式;
(2)当点C在⊙O上运动到什么位置时,AC与⊙O相切?请说明理由.
(3)直线AB经过怎样的平移后与⊙O相切?请写出计算过程加以说明.
分析 (1)设直线AB的解析式为y=kx+b,利用待定系数法即可解决问题;
(2)如图1中,设直线AC与⊙O相切于点C,连接OC,作CH⊥OA于H.利用面积法求出点C坐标,再根据对称性确定另一个点C′的坐标即可;
(3)如图2中,作OM⊥AB于M交⊙O于G、N.求出MN、GM的长即可解决问题;
解答 解:(1)设直线AB的解析式为y=kx+b,则有$\left\{\begin{array}{l}{6k+b=0}\\{b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴直线AB的解析式为y=-x+6.
(2)如图1中,设直线AC与⊙O相切于点C,连接OC,作CH⊥OA于H.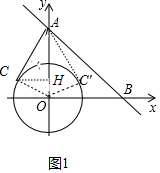
∵AC是切线,
∴∠ACO=90°,
∵OC=2$\sqrt{2}$,OA=6,
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{36-8}$=2$\sqrt{7}$,
∵S△ACO=$\frac{1}{2}$•AC•CO=$\frac{1}{2}$•OA•CH,
∴CH=$\frac{2\sqrt{14}}{3}$,
∴OH=$\sqrt{O{C}^{2}-C{H}^{2}}$=$\frac{4}{3}$,
∴点C坐标为(-$\frac{2\sqrt{14}}{3}$,$\frac{4}{3}$),
根据对称性可知当点C′坐标为($\frac{2\sqrt{14}}{3}$,$\frac{4}{3}$)时,直线AC′也是⊙O的切线.
综上所述,满足条件的点C坐标为(-$\frac{2\sqrt{14}}{3}$,$\frac{4}{3}$)或($\frac{2\sqrt{14}}{3}$,$\frac{4}{3}$).
(3)如图2中,作OM⊥AB于M交⊙O于G、N.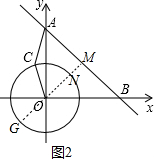
易知:OM=$\frac{1}{2}$AB=3$\sqrt{2}$,
∴MN=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$,GM=3$\sqrt{2}$+2$\sqrt{2}$=5$\sqrt{2}$,
∴直线AB沿第一象限和第三象限的角平分线方向,向下平移$\sqrt{2}$或5$\sqrt{2}$个单位后与⊙O相切.
点评 本题考查一次函数的应用、圆、切线的判定和性质、勾股定理、三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用面积法确定点的坐标,属于中考压轴题.

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法: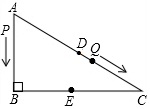 如图,在Rt△ABC中,∠B=90°,∠C=30°,AB=12厘米,点P从A出发沿线路AB-BC作匀速运动,点Q从AC的中点D同时出发沿线路DC-CB作匀速运动逐步靠近点P.设两点P、Q的速度分别为1厘米/秒、a厘米/秒(a>1),它们在t秒后于BC边上的某一点E相遇.
如图,在Rt△ABC中,∠B=90°,∠C=30°,AB=12厘米,点P从A出发沿线路AB-BC作匀速运动,点Q从AC的中点D同时出发沿线路DC-CB作匀速运动逐步靠近点P.设两点P、Q的速度分别为1厘米/秒、a厘米/秒(a>1),它们在t秒后于BC边上的某一点E相遇. 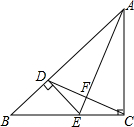 已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E作ED⊥AB于D,连接DC交AE于F,其中BD=1,下列结论:①DC⊥AE;②AB=2+$\sqrt{2}$;③CD•AE=2$\sqrt{2}$+2;④$\frac{AE}{CD}$=2:1,其中正确的结论是①②③.
已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E作ED⊥AB于D,连接DC交AE于F,其中BD=1,下列结论:①DC⊥AE;②AB=2+$\sqrt{2}$;③CD•AE=2$\sqrt{2}$+2;④$\frac{AE}{CD}$=2:1,其中正确的结论是①②③.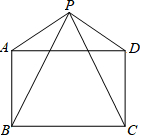 如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.
如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.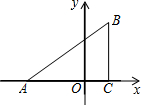 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.