题目内容
3.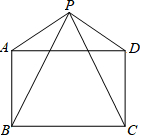 如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.
如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.(1)求证:∠ABC=∠DCB;
(2)求证:四边形ABCD是矩形.
分析 (1)由全等三角形的判定定理SAS推知△ABP≌△DCP,根据该全等三角形的对应角相等、等腰三角形的性质推知∠ABC=∠DCB;
(2)由“有一内角是直角的平行四边形为矩形”证得结论.
解答 (1)证明:在△ABP和△DCP中,
$\left\{\begin{array}{l}{PA=PD}\\{∠APB=∠DPC}\\{PB=PC}\end{array}\right.$
∴△ABP≌△DCP(SAS).
∴∠ABP=∠DCP.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABP+∠PBC=∠DCP+∠PCB.
即∠ABC=∠DCB;
(2)证明:∵△ABP≌△DCP,
∴AB=CD.
∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AB∥DC.
∴∠ABC+∠DCB=180°.
∵∠ABC=∠DCB,
∴2∠ABC=180°.即∠ABC=90°.
∴四边形ABCD是矩形.
点评 此题主要考查了矩形的判定,全等三角形的判定与性质以及等腰三角形的性质,关键是掌握有一内角是直角的平行四边形为矩形.

练习册系列答案
相关题目
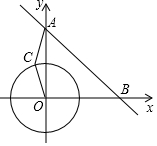 在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.
在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC. [问题提出]
[问题提出]