��Ŀ����
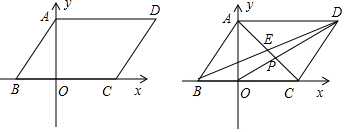
2��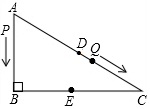 ��ͼ����Rt��ABC�У���B=90�㣬��C=30�㣬AB=12���ף���P��A��������·AB-BC�������˶�����Q��AC���е�Dͬʱ��������·DC-CB�������˶�������P��������P��Q���ٶȷֱ�Ϊ1����/�롢a����/�루a��1����������t�����BC���ϵ�ijһ��E������
��ͼ����Rt��ABC�У���B=90�㣬��C=30�㣬AB=12���ף���P��A��������·AB-BC�������˶�����Q��AC���е�Dͬʱ��������·DC-CB�������˶�������P��������P��Q���ٶȷֱ�Ϊ1����/�롢a����/�루a��1����������t�����BC���ϵ�ijһ��E������ ��1�����AC��BC�ij��ȣ�
��2��������������ʱ���ڵ�E�����BC���е���Ϊʲô��
��3������D��E��CΪ��������������ABC���ƣ��Էֱ����a��t��ֵ���������ȷ��0.1��
���� ��1��������֪���������Ǻ����Ϳ��Եó�AC��BC�ij��ȣ�
��2����t���Q�˶���·��Ϊat����P�˶���·��Ϊt����ô��BE=t-12��CE=at-12��������ʽ����ȵ�t��ֵ�����ڣ�
��3����D��E��CΪ��������������ABC���ƣ����ڡ�C=��C���֡�DEC=��B=90����E'DC=��B=90������������ۼ��㼴�ɵó����ۣ�
��� �⣺��1����Rt��ABC�У���B=90�㣬��C=30�㣬AB=12���ף�
��AC=2AB=24�����ף���
��BC=$\sqrt{3}$AB=12$\sqrt{3}$�����ף���
��2��E�㲻����BC���е㣮
��t���Q�˶���·��Ϊat����P�˶���·��Ϊt����ô
BE=t-12��CE=at-12��
��a��1��
��at-12��t-12��
��E�㲻����BC���е㣮
��3������D��E��CΪ��������������ABC���ƣ�
�ߡ�C=��C��
���DEC=��B=90����E'DC=��B=90�㣬
�ٵ���DEC=��B=90��ʱ����CDE�ס�CAB��
��$\frac{CE}{CB}=\frac{CD}{AC}$
��$\frac{CE}{12\sqrt{3}}=\frac{12}{24}$
��CE=6$\sqrt{3}$��
��BE=BC-CE=6$\sqrt{3}$��
��BE=t-AB=t-12=6$\sqrt{3}$
��t=12+6$\sqrt{3}$��
��CE=at-CD=at-12=6$\sqrt{3}$��
��a=$\frac{12+6\sqrt{3}}{t}$=$\frac{12+6\sqrt{3}}{12+6\sqrt{3}}$=1��
��a��1��
�����������������⣬
�ڵ���E'DC=��B=90��ʱ��
�����DCE'�ס�BCA��
��$\frac{CE'}{AC}=\frac{CD}{BC}$
��$\frac{CE'}{24}=\frac{12}{12\sqrt{3}}$��
��CE'=24��$\frac{\sqrt{3}}{3}$=8$\sqrt{3}$��
��BC=12$\sqrt{3}$��
��BE'=BC-CE'=12$\sqrt{3}$-8$\sqrt{3}$=4$\sqrt{3}$��
���˶�֪��CE'=at-12��BE'=t-12��
��at-12=8$\sqrt{3}$��t-12=4$\sqrt{3}$��
��t=12+4$\sqrt{3}$��18.9��a=$\frac{\sqrt{3}+1}{2}$��1.4
��t=18.9�룬a=1.4����/�룮
���� ���������������ε��ۺ��⣬��Ҫ�����˺�30���ֱ�������ε����ʣ����������ε��ж������ʣ��Ȿ��Ĺؼ����÷������۵�˼��˼�����⣮

| A�� | PQ��9 | B�� | PQ��9 | C�� | PQ��9 | D�� | PQ��9 |
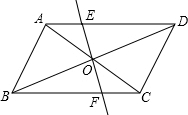 ��ͼ����֪O��?ABCD�ĶԽ��ߵĽ��㣬����O��ֱ�߷ֱ���AD��BC�ཻ�ڵ�E��F����֤��OE=OF��
��ͼ����֪O��?ABCD�ĶԽ��ߵĽ��㣬����O��ֱ�߷ֱ���AD��BC�ཻ�ڵ�E��F����֤��OE=OF��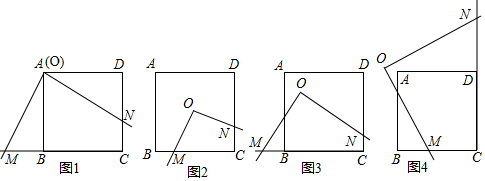
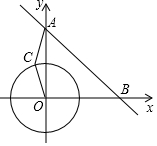 ��ƽ��ֱ������ϵxOy�У���֪��A��0��6������B��6��0��������C���뾶Ϊ2$\sqrt{2}$�ġ�O�ϣ�����OC��AC��
��ƽ��ֱ������ϵxOy�У���֪��A��0��6������B��6��0��������C���뾶Ϊ2$\sqrt{2}$�ġ�O�ϣ�����OC��AC��