题目内容
10.已知A=a2+b2-c2,B=-4a2+2b2+3c2,且A+B+C=0.求:(1)多项式C;
(2)若a,b,c满足(a-1)2+(b+1)2+|c-3|=0时,求A+B的值.
分析 (1)把A,B代入A+B+C=0中表示出C即可;
(2)利用非负数的性质求出a,b,c的值,代入A+B中计算即可得到结果.
解答 解:(1)∵A=a2+b2-c2,B=-4a2+2b2+3c2,
∴C=-(A+B)=-(a2+b2-c2-4a2+2b2+3c2)=3a2-3b2-2c2;
(2)∵(a-1)2+(b+1)2+|c-3|=0,
∴a=1,b=-1,c=3,
则A+B=a2+b2-c2-4a2+2b2+3c2=-3a2+3b2+2c2=-3+3+18=18.
点评 此题考查了整式的加减,以及整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18. 如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.
如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.
 如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.
如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为( )cm2.| A. | 8$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
15. 下列各展开图中,不能折成如图长方体的是( )
下列各展开图中,不能折成如图长方体的是( )
 下列各展开图中,不能折成如图长方体的是( )
下列各展开图中,不能折成如图长方体的是( )| A. |  | B. |  | C. |  | D. |  |
2.用配方法解方程x2+8x-7=0,则配方正确的是( )
| A. | (x+4)2=23 | B. | (x-4)2=23 | C. | (x-8)2=49 | D. | (x+8)2=64 |
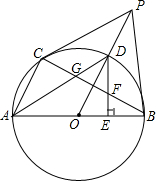 如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G
如图,AB为直径,PB为切线,点C在⊙O上,AC∥OP,连接OP,交⊙O点D,交BC于点H,过D点作DE⊥AB,E为垂足,交BC于点F,连AD交BC于G