题目内容
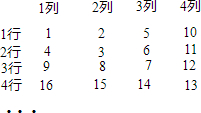
14.观察图中数的排列规律:(1)第6行第1列的数是多少?
(2)70在第几行第几列?
(3)2015在第几行第几列?为什么?
(4)请用含n的式子表示第n行第n列的数.
分析 (1)观察每行的第一个数,根据数的变化找出规律“第n行第1列的数是n2”,依次规律即可得出结论;
(2)观察每行(列)的数,发现规律“第n行(列)有n个连续的数,且数字的排列顺序是先列后行(从上往下,从右往左)”,依次规律即可解决问题;
(3)结合(1)(2)的规律,再根据“2025=452,2015=2025-10”,即可得出结论;
(4)结合(1)(2)的规律,即可得出结论.
解答 解:(1)观察,发现规律:第1行第1列的数是1,第2行第1列的数是4,第3行第1列的数是9,…,
∴第n行第1列的数是n2.
当n=6时,
第6行第1列的数是62=36.
(2)观察发现第n行(列)有n个连续的数,且数字的排列顺序是先列后行(从上往下,从右往左),
∵82=64,70-64=6,
∴70在第6行第9列.
(3)∵2025=452,2015=2025-10,
∴2015在第45行第35列.
理由为:第n行(列)有n个连续的数,且数字的排列顺序是先列后行(从上往下,从右往左).
(4)结合(1)与(2)即可值:
第n行第1列的数是n2,第n行第n列的数是n2-n+1.
点评 本题考查了规律型中的数字的变化类,解题的关键是:(1)找出规律“第n行第1列的数是n2”;(2)找出规律“第n行(列)有n个连续的数,且数字的排列顺序是先列后行(从上往下,从右往左)”;(3)找出2025=452,2015=2025-10;(4)利用(1)(2)的规律.本题属于中档题,难度不大,解决该题型题目时,结合数字的排布方式,找出规律是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.为了解某社区居民的用电情况,随机对该社区15户居民进行调查,下表是这15户居民2015年4月份用电量的调查结果:
那么关于这15户居民月用电量(单位:度),下列说法错误的是( )
| 居民(户) | 5 | 3 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 平均数是43.25 | B. | 众数是30 | C. | 方差是82.4 | D. | 中位数是42 |
6.(x2+mx+1)(x-3)的积中x的二次项系数为零,则m的值是( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
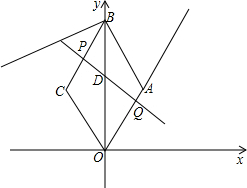 已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.
已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.
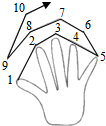 如图,我们做一个游戏:从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指…的顺序依次数正整数1、2、3、4、5…,当第(n+1)次数到中指时,恰好数到的数是3+4n(用含n的代数式表示).
如图,我们做一个游戏:从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指…的顺序依次数正整数1、2、3、4、5…,当第(n+1)次数到中指时,恰好数到的数是3+4n(用含n的代数式表示). 如图,△ABC中,∠BAC=90°,将△ABC绕点A按顺时针方向旋转一定角度得到∠ADE,点B的对应点D恰好落在BC边上,若AC=2$\sqrt{3}$,∠B=60°,则CD的长为( )
如图,△ABC中,∠BAC=90°,将△ABC绕点A按顺时针方向旋转一定角度得到∠ADE,点B的对应点D恰好落在BC边上,若AC=2$\sqrt{3}$,∠B=60°,则CD的长为( )