题目内容
4. 如图,△ABC中,∠BAC=90°,将△ABC绕点A按顺时针方向旋转一定角度得到∠ADE,点B的对应点D恰好落在BC边上,若AC=2$\sqrt{3}$,∠B=60°,则CD的长为( )
如图,△ABC中,∠BAC=90°,将△ABC绕点A按顺时针方向旋转一定角度得到∠ADE,点B的对应点D恰好落在BC边上,若AC=2$\sqrt{3}$,∠B=60°,则CD的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 2$\sqrt{2}$ |
分析 先在直角三角形ABC中,求出AB,BC,然后判断出BD=AB=2,简单计算即可.
解答 解:在Rt△ABC中,AC=2$\sqrt{3}$,∠B=60°,
∴AB=2,BC=4,
由旋转得,AD=AB,
∵∠B=60°,
∴BD=AB=2,
∴CD=BC-BD=4-2=2,
故选B.
点评 此题是旋转的性质题,主要考查了旋转的性质,直角三角形的性质,解本题的关键是判断出BD=AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若x,y为实数,且$\sqrt{2x+y}$+(x-y+3)2=0,则x+y的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 5 |
19.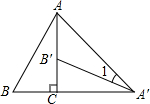 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )| A. | 84° | B. | 72° | C. | 63° | D. | 54° |
 如图,△ABC绕A逆时针旋转使得C点落在BC边上的F处,则对于结论:
如图,△ABC绕A逆时针旋转使得C点落在BC边上的F处,则对于结论: