题目内容
12.已知x=1是方程x2-3ax+a2=0的一个根,求代数式3a2-9a+1的值.分析 根据方程解的定义,把x=1代入得出关于a的方程,求得a的值,再代入即可得出答案.
解答 解:∵x=1是方程x2-3ax+a2=0的一个根,
∴1-3a+a2=0.
∴a2-3a=-1.
∴3a2-9a+1=3(a2-3a)+1=3×(-1)+1=-2.
或
解:∵x=1是方程x2-3ax+a2=0的一个根,
∴1-3a+a2=0.
∴a2-3a+1=0.
解方程得$a=\frac{{3±\sqrt{5}}}{2}$.
把$a=\frac{{3±\sqrt{5}}}{2}$代入得3a2-9a+1得3a2-9a+1=-2.
点评 本题考查了一元二次方程的解,有方程的解得出a的值是解题的关键.

练习册系列答案
相关题目
3.不等式x+3<2的解集是( )
| A. | x<1 | B. | x<-1 | C. | x>1 | D. | x>-1 |
20.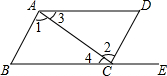 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )
①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
| A. | ①或④ | B. | ②或③ | C. | ①或③ | D. | ②或④ |
7.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.某校本学年开展了读书活动,在这次活动中,八年级(1)班40名学生读书册数的情况如表:
根据表中的数据,求:
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.
| 读书册数 | 4 | 5 | 6 | 7 | 8 |
| 人数(人) | 6 | 4 | 10 | 12 | 8 |
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.
4.下列命题中,真命题的个数是( )
①同位角相等;
②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c.
③a,b,c是三条直线,若a∥b,b∥c,则a∥c;
④过一点有且只有一条直线与已知直线平行.
①同位角相等;
②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c.
③a,b,c是三条直线,若a∥b,b∥c,则a∥c;
④过一点有且只有一条直线与已知直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列式子中,正确的是( )
| A. | x3÷x2=x | B. | x3+x2=x5 | C. | x3-x2=x | D. | x3•x2=x6 |
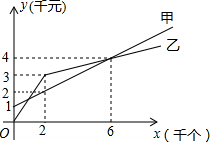 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费 黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).
黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).