题目内容
14. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
分析 (1)只要证明∠DBF=∠DAC,即可判断.
(2)利用相似三角形的性质即可解决问题.
解答 (1)证明:如图,∵AD⊥BC,BE⊥AC
∴∠BDF=∠ADC=∠BEC=90°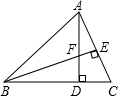
∴∠C+∠DBF=90°,∠C+∠DAC=90°
∴∠DBF=∠DAC
∴△ACD∽△BFD;
(2)解:如图,∵∠ABD=45°,∠ADB=90°,
∴AD=BD,
∴$\frac{AD}{BD}$=1,
∵△ACD∽△BFD,AC=3,
∴$\frac{AC}{BF}=\frac{AD}{BD}$=1,
∴BF=AC=3.
点评 本题考查相似三角形的性质和判定,同角的余角相等,直角三角形两锐角互余等知识,解题的关键是正确寻找相似三角形,利用新三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
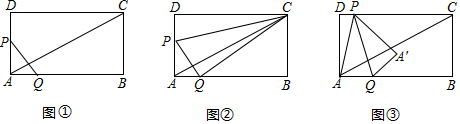
6.图中,∠1与∠2是同位角的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 如图,AB是半圆O的直径,∠BAC=35°,则∠D的大小是125度.
如图,AB是半圆O的直径,∠BAC=35°,则∠D的大小是125度.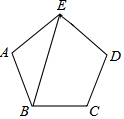 如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.
如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.