题目内容
3.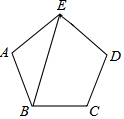 如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.
如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.
分析 首先利用多边形的内角和公式求得正五边形的内角和,再求得每个内角的度数,利用等腰三角形的性质可得∠BAE的度数,易得∠CAE.
解答 解:正五边形内角和:(5-2)×180°=3×180°=540°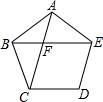
∴∠ABC=∠BAE=$\frac{540°}{5}$=108°,
∴∠BAE=$\frac{180°-∠ABC}{2}$=$\frac{180°-108°}{2}$=36°,
∴∠CAE=∠BAE-∠BAC=108°-36°=72°.
点评 本题主要考查了正多边形的内角和,熟记多边形的内角和公式:(n-2)×180°是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列事件:①随意翻到一本书的某页,这页的页码是奇数;②测得某天的最高气温是100℃;③掷一次骰子,向上一面的数字是2;④度量四边形的内角和,结果是360°.其中随机事件有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.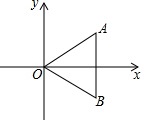 如图,△ABO关于x轴对称,若点A的坐标为(3,1),则点B的坐标为( )
如图,△ABO关于x轴对称,若点A的坐标为(3,1),则点B的坐标为( )
 如图,△ABO关于x轴对称,若点A的坐标为(3,1),则点B的坐标为( )
如图,△ABO关于x轴对称,若点A的坐标为(3,1),则点B的坐标为( )| A. | (1,3) | B. | (-1,3) | C. | (3,-1) | D. | (-1,-3) |
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.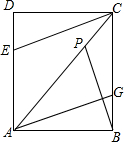 如图,矩形ABCD中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).
如图,矩形ABCD中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).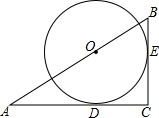 如图,△ABC中,∠C=90°,以AB上一点O为圆心的⊙O分别与AC、BC相切于D,E,若AC=4,BC=3,求⊙O的半径.
如图,△ABC中,∠C=90°,以AB上一点O为圆心的⊙O分别与AC、BC相切于D,E,若AC=4,BC=3,求⊙O的半径. 如图,在平面直角坐标系中,四边形OADC是矩形,OA=6,AB=4,直线y=-x+3与坐标轴交于D,E.设M是AB的中点,P是线段DE上的动点,
如图,在平面直角坐标系中,四边形OADC是矩形,OA=6,AB=4,直线y=-x+3与坐标轴交于D,E.设M是AB的中点,P是线段DE上的动点,