题目内容
2．在△ABC中，∠C=90°，sinA=$\frac{3}{4}$，AB=8cm，则AC的长是2$\sqrt{7}$cm．分析 根据三角函数的定义即可得出BC=6cm，再由勾股定理得出AC的长即可．
解答 解：∵∠C=90°，
∴sinA=$\frac{BC}{AB}$=$\frac{3}{4}$，
∵AB=8cm，
∴BC=6cm，
∴AC=2$\sqrt{7}$cm，
故答案为2$\sqrt{7}$．
点评 本题考查了解直角三角形以及三角函数的定义，掌握勾股定理和三角函数的定义是解题的关键．
练习册系列答案
相关题目
12．已知点（2，y1），（-3，y2）均在抛物线y=x2-1上，则y1、y2的大小关系为（ ）
| A． | y1＜y2 | B． | y1＞y2 | C． | y1≤y2 | D． | y1≥y2 |
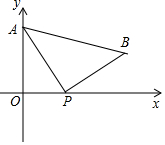如图，A（0，4）是直角坐标系y轴上一点，动点P从原点O出发，沿x轴正半轴运动，速度为每秒1个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB．设P点的运动时间为t秒．
17．若一元二次方程x2-2x+3m=0有两个相等的实数根，则方程mx2+2x+8m=0的解是（ ）
| A． | $\frac{1}{3}$ | B． | 2或4 | C． | -2或-4 | D． | -2或4 |
如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D、E，AD与BE相交于点F．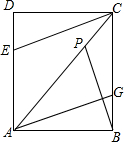
如图，矩形ABCD中，∠ABC=90°，AB=6cm，BC=8cm，动点P从点C出发，在线段AC上以每秒5cm的速度向点A匀速运动，同时动点Q从点B出发，在BC边上以每秒4cm的速度向点C匀速运动，动点E从点D出发，在DA边上以每秒4cm的速度向点A匀速运动，运动时间为t秒（0＜t＜2）．