题目内容
2. 在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )
在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )| A. | k≤$\frac{4}{3}$ | B. | -$\frac{4}{3}$≤k≤-$\frac{1}{7}$ | C. | -$\frac{4}{3}$≤k≤-1 | D. | -$\frac{4}{3}$≤k≤$\frac{4}{3}$ |
分析 首先根据正方形的性质求出B、C点的坐标,分别把B和C点坐标代入y=kx+4求出对应的k的值,然后写出满足条件的k的取值范围.
解答 解:∵四边形ABCD为正方形,点A(0,4),B(3,0),
∴C点坐标为(7,3)
把B(3,0)代入y=kx+4得3k+4=0,解得k=$-\frac{4}{3}$;把C(7,3)代入y=kx+4得7k+4=3,解得k=-$\frac{1}{7}$,
所以当直线y=kx+4与线段BC有交点时,k的取值范围为-$\frac{4}{3}$≤k≤$-\frac{1}{7}$.
故选B.
点评 本题考查了两条直线相交或平行问题,根据正方形的性质得出C点的坐标是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.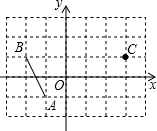 如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )
如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )
 如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )
如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )| A. | (3,2) | B. | (2,1) | C. | (1,3) | D. | (2,3) |
14.8的负的平方根介于( )
| A. | -5与-4之间 | B. | -4与-3之间 | C. | -3与-2之间 | D. | -2与-1之间 |
12.若|x-2y-1|+|2x-y-5|=0,则x+y的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |

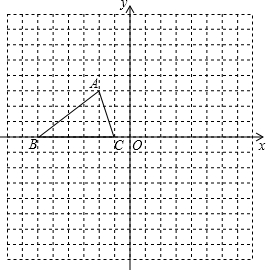 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).