题目内容
10.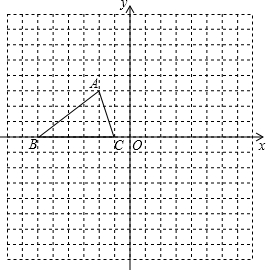 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1,图中画出△A1B1C1,平移后点A的对应点A1的坐标是(3,-1).
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是(-2,-3).
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为13.5.
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用关于x轴对称点的性质进而得出对应点位置;
(3)利用平移的性质可得△ABC扫过的面积为△A′B′C′+平行四边形A′C′CA的面积.
解答 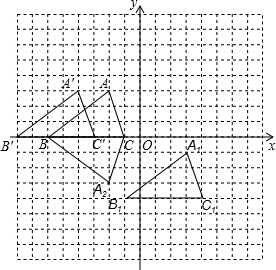 解:(1)如图所示:△A1B1C1,即为所求,平移后点A的对应点A1的坐标是:(3,-1);
解:(1)如图所示:△A1B1C1,即为所求,平移后点A的对应点A1的坐标是:(3,-1);
故答案为:(3,-1);
(2)如图所示:△A2BC,即为所求,翻折后点A对应点A2坐标是:(-2,-3);
故答案为:(-2,-3);
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为:
S△A′B′C′+S平行四边形A′C′CA
=$\frac{1}{2}$×3×5+2×3
=13.5.
故答案为:13.5.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出平移后对应点位置是解题关键.

练习册系列答案
相关题目
20.在△ABC中,∠ACB=90°,∠ABC=25°,O为AB边的中点,将OA绕点O逆时针旋转一个锐角得到线段OD,连接BD、CD,若△BCD为轴对称图形,则∠AOD的度数为50°或65°或80°.
5.一等腰梯形中,高为2,下底为4,下底的底角正弦值为$\frac{4}{5}$,那么它的上底和腰长分别为( )
| A. | 2,$\frac{5}{2}$ | B. | 1,$\frac{5}{2}$ | C. | 1,2 | D. | 2,5 |
2. 在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )
在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )
 在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )
在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )| A. | k≤$\frac{4}{3}$ | B. | -$\frac{4}{3}$≤k≤-$\frac{1}{7}$ | C. | -$\frac{4}{3}$≤k≤-1 | D. | -$\frac{4}{3}$≤k≤$\frac{4}{3}$ |
19. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )
 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )| A. | 1<b<8 | B. | 1≤b≤8 | C. | 2≤b≤8 | D. | 2≤b<8 |
20.已知a、b为两个连续整数,且a<$\sqrt{7}$<b,则a+b的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 如图,四边形ABCD是直角梯形,∠C=90°,AO⊥BC于点O.A、B、C、D、O分别在边长为I的小正方形网格上.以O为原点,BC所在直线为x轴,建立平面直角坐标系.
如图,四边形ABCD是直角梯形,∠C=90°,AO⊥BC于点O.A、B、C、D、O分别在边长为I的小正方形网格上.以O为原点,BC所在直线为x轴,建立平面直角坐标系.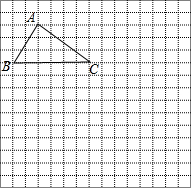 △ABC在网格中的位置如图所示,请根据下列要求解答:
△ABC在网格中的位置如图所示,请根据下列要求解答: