题目内容
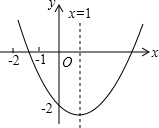 已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论:①2a+b>0;②b2-8a>4ac;③8a+c>0;④9a+3b+c<0.
正确的有
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:①由图知:抛物线开口向上,得:a>0;
抛物线的对称轴为x=-
=1,b=-2a,则2a+b=0故①错误;
②抛物线交y轴于负半轴,得:c=-2;因为b=-2a,
所以b2-8a=4a2-8a,4ac=-8a,
因为4a2>0,所以4a2-8a>-8a,
所以b2-8a>4ac,故②正确;
③根据①可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故③正确;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
所以这四个结论都正确.
故答案为①②③④.
抛物线的对称轴为x=-
| b |
| 2a |
②抛物线交y轴于负半轴,得:c=-2;因为b=-2a,
所以b2-8a=4a2-8a,4ac=-8a,
因为4a2>0,所以4a2-8a>-8a,
所以b2-8a>4ac,故②正确;
③根据①可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故③正确;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
所以这四个结论都正确.
故答案为①②③④.
点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图,在△ABC中,AD是边BC上的高,AC=BD,已知sinC=
如图,在△ABC中,AD是边BC上的高,AC=BD,已知sinC=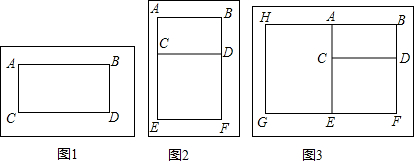
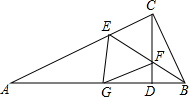 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.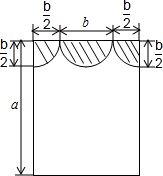 如图,小红家装饰新家,小红为自己的房间选择了一款窗帘,请你帮她计算:
如图,小红家装饰新家,小红为自己的房间选择了一款窗帘,请你帮她计算: