题目内容
在线段AB中找出点C,使其满足
=
,则C为线段AB的黄金分割点.若使AB为长方形的长,AC为长方形的宽,则其为黄金矩形.
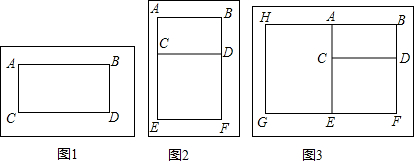
(1)长方形ABDC为黄金矩形,面积为15,求AB和AC的长度;
(2)长方形ABEF为黄金矩形(长方形ABDC就是图1的长方形),求AE长;
(3)长方形BFGH为黄金矩形(长方形ABEF就是图2的长方形),求GF长;
(4)若继续按下面的方法画下去,可以得到第四个、第五个、第六个…求第十个这样的黄金矩形的长.
| AC |
| AB |
| BC |
| AC |

(1)长方形ABDC为黄金矩形,面积为15,求AB和AC的长度;
(2)长方形ABEF为黄金矩形(长方形ABDC就是图1的长方形),求AE长;
(3)长方形BFGH为黄金矩形(长方形ABEF就是图2的长方形),求GF长;
(4)若继续按下面的方法画下去,可以得到第四个、第五个、第六个…求第十个这样的黄金矩形的长.
考点:黄金分割
专题:
分析:(1)由黄金分割的定义设AB=x,则AC=
x,根据长方形ABDC的面积为15列出方程,解方程即可;
(2)由
=
及AB=
,即可求出AE的长;
(3)由
=
及BF=AE=
即可求出GF的长;
(4)根据前面的方法,即可求出第四个、第五个、第六个…第十个这样的黄金矩形的长.
| ||
| 2 |
(2)由
| AB |
| AE |
| ||
| 2 |
| ||||
| 2 |
(3)由
| BF |
| GF |
| ||
| 2 |
(
| ||||||
| 4 |
(4)根据前面的方法,即可求出第四个、第五个、第六个…第十个这样的黄金矩形的长.
解答:解:(1)如图1,设AB=x,则AC=
x,
x•
x=15,
解得x=±
(负值舍去),
所以AB=
,AC=
×
=
;
(2)如图2,∵
=
,AB=
,
∴AE=
=
×
=
;
(3)如图3,∵
=
,BF=AE=
,
∴GF=
BF=
×
=
;
(4)第四个黄金矩形的长为(
)3×
,
第五个黄金矩形的长为(
)4×
,
第六个黄金矩形的长为(
)5×
,
…,
第十个黄金矩形的长为(
)9×
.
| ||
| 2 |
x•
| ||
| 2 |
解得x=±
| ||||
| 2 |
所以AB=
| ||||
| 2 |
| ||
| 2 |
| ||||
| 2 |
(
| ||||||
| 4 |
(2)如图2,∵
| AB |
| AE |
| ||
| 2 |
| ||||
| 2 |
∴AE=
| 2AB | ||
|
| 2 | ||
|
| ||||
| 2 |
(
| ||||||
| 4 |
(3)如图3,∵
| BF |
| GF |
| ||
| 2 |
(
| ||||||
| 4 |
∴GF=
| 2 | ||
|
| 2 | ||
|
(
| ||||||
| 4 |
(3+
| ||||||
| 4 |
(4)第四个黄金矩形的长为(
| 2 | ||
|
| ||||
| 2 |
第五个黄金矩形的长为(
| 2 | ||
|
| ||||
| 2 |
第六个黄金矩形的长为(
| 2 | ||
|
| ||||
| 2 |
…,
第十个黄金矩形的长为(
| 2 | ||
|
| ||||
| 2 |
点评:本题考查了黄金分割的定义:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
)叫做黄金比.
| ||
| 2 |

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
下列说法正确的是( )
| A、同号两数相乘,取原来的符号 |
| B、一个数与-1相乘,积为该数的相反数 |
| C、一个数与0相乘仍得这个数 |
| D、两个数相乘,积大于任何一个乘数 |
 如图,已知PA是⊙O的切线,P为切点,PA=5
如图,已知PA是⊙O的切线,P为切点,PA=5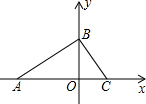 已知:如图,在平面直角坐标系中,点A,B分别在x,y轴上,且OA,OB的长(OA>OB)是一元二次方程x2-7x+12=0的两根.
已知:如图,在平面直角坐标系中,点A,B分别在x,y轴上,且OA,OB的长(OA>OB)是一元二次方程x2-7x+12=0的两根. 如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,图中有哪些相等的线段?
如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,图中有哪些相等的线段?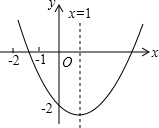 已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论: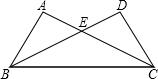 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.