题目内容
10.有A,B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3;B布袋中有三个标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.若用(m,n)表示小明取球时m与n的对应值,则使关于x的一元二次方程x2-mx+$\frac{1}{2}$n=0有实数根的概率为$\frac{2}{3}$.分析 依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可.
解答 解:画树形图得: .
.
∴(m,n)所有取值是(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2);
由原方程得;△=m2-2n.
当m,n对应值为(0,0)(1,0),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)时,△≥0,原方程有实数根.
所以P(△≥0)=$\frac{8}{12}$=$\frac{2}{3}$
故答案为:$\frac{2}{3}$.
点评 此题主要考查了列表法求概率以及根的判别式的运用,解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.在下列四个图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.下列四个实数中,最大的是( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 0 | D. | -1 |
 如图,在矩形ABCD中,BC=10,AB=4,动点E从点B出发沿BC向终点C以每秒1个单位长度的速度运动,动点F沿折线BA-AD向终点D以每秒2个单位长度的速度运动,过点E作BF的平行线与过点F作BE的平行线相交于点G,若点E,F同时出发,当有一个点到达终点时,另一个点继续运动直至到达终点停止,四边形BEGF与矩形ABCD重叠部分的面积为S(平方单位),运动的时间为t(秒).
如图,在矩形ABCD中,BC=10,AB=4,动点E从点B出发沿BC向终点C以每秒1个单位长度的速度运动,动点F沿折线BA-AD向终点D以每秒2个单位长度的速度运动,过点E作BF的平行线与过点F作BE的平行线相交于点G,若点E,F同时出发,当有一个点到达终点时,另一个点继续运动直至到达终点停止,四边形BEGF与矩形ABCD重叠部分的面积为S(平方单位),运动的时间为t(秒).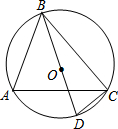 如图,⊙O的直径BD=4,∠A=60°,则BC的长度为2$\sqrt{3}$.
如图,⊙O的直径BD=4,∠A=60°,则BC的长度为2$\sqrt{3}$. 如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)
如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)