题目内容
12.(1)已知x-1=$\sqrt{3}$,求代数式(x+1)2-4(x+1)+4的值;(2)已知a,b满足$\sqrt{2a+8}$+|b-$\sqrt{3}$|=0,解关于x的方程(a+2)x+b2=a-1.
分析 (1)原式利用完全平方公式变形,将已知等式代入计算即可求出值;
(2)根据已知等式,利用非负数的性质求出a与b的值,代入方程计算即可求出解.
解答 解:(1)∵x-1=$\sqrt{3}$,
∴原式=(x+1-2)2=(x-1)2=3;
(2)∵$\sqrt{2a+8}$+|b-$\sqrt{3}$|=0,
∴a=-4,b=$\sqrt{3}$,
代入方程得:-2x+3=-5,
解得:x=4.
点评 此题考查了因式分解-运用公式法,非负数的性质,以及解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.
如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.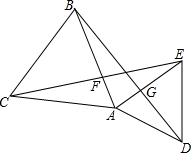 已知△ABC和△DAE是等边三角形,CE与AB交于点F,BD与AE交于点G,试问CE=BD吗?请说明你的结论.
已知△ABC和△DAE是等边三角形,CE与AB交于点F,BD与AE交于点G,试问CE=BD吗?请说明你的结论.