题目内容
9.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;
(2)当t为多少时.△PQB是以BP为底的等腰三角形.
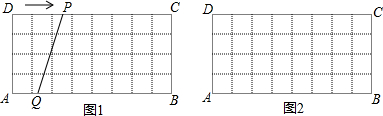
分析 (1)根据点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位可知,当t=6秒时,DP=6,AQ=3即可画出线段PQ;
(2)设时间为t,则在t秒钟,P运动了t个单位,Q运动了$\frac{1}{2}$t个单位,由题意得 PQ=BQ,然后根据勾股定理列出关于t的方程,解得t即可.
解答 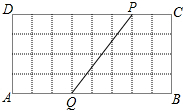 解:(1)如图所示,由勾股定理得PQ=$\sqrt{{3}^{2}+{4}^{2}}$=5;
解:(1)如图所示,由勾股定理得PQ=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)设时间为t,则在t秒钟,P运动了t格,Q运动了$\frac{1}{2}$t格,由题意得PQ=BQ,
即(t-$\frac{1}{2}$t)2+42=(8-$\frac{1}{2}$t)2,解得t=6(秒).
答:当t为6秒时.△PQB是以BP为底的等腰三角形.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
14.当n为偶数时,(a-b)m•(b-a)n与(b-a)m+n的关系是( )
| A. | 相等 | |
| B. | 互为相反数 | |
| C. | 当m为偶数时互为相反数,当m为奇数时相等 | |
| D. | 当m为偶数时相等,当m为奇数时为互为相反数 |
18.先列方程,在估算出方程的解
甲型钢笔每支3元,乙型钢笔每支5元,用40元钱买了两种钢笔共10支,还多2元,问两种钢笔各买了多少支?
解:设买了甲型铅笔x支,则乙型钢笔10-x支,依题意得方程:3x+5(10-x)=40-2.
这里x>0,列表如下:
从表中看出x=6是原方程的解.
甲型钢笔每支3元,乙型钢笔每支5元,用40元钱买了两种钢笔共10支,还多2元,问两种钢笔各买了多少支?
解:设买了甲型铅笔x支,则乙型钢笔10-x支,依题意得方程:3x+5(10-x)=40-2.
这里x>0,列表如下:
| x(支) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3x+5(10-x)(元) | 48 | 46 | 44 | 42 | 40 | 38 | 36 | 34 |
 如图,长方形ABCD的长是a,宽是b,分别以A,B为圆心,b为半径作圆,交AB于点E,F,列式表示阴影部分的周长l和面积S.
如图,长方形ABCD的长是a,宽是b,分别以A,B为圆心,b为半径作圆,交AB于点E,F,列式表示阴影部分的周长l和面积S.