题目内容
14．当n为偶数时，（a-b）m•（b-a）n与（b-a）m+n的关系是（ ）| A． | 相等 | |
| B． | 互为相反数 | |
| C． | 当m为偶数时互为相反数，当m为奇数时相等 | |
| D． | 当m为偶数时相等，当m为奇数时为互为相反数 |
分析 根据互为相反数的偶数次幂相等，互为相反数的奇数次幂互为相反数，可得同底数幂的乘法，根据同底数幂的乘法，可得答案．
解答 解：当m为偶数时，（a-b）m•（b-a）n=（b-a）m•（b-a）n=（b-a）m+n，
当m为奇数时，（a-b）m•（b-a）n=-（b-a）m•（b-a）n=-（b-a）m+n与（b-a）m+n互为相反数，
故选：D．
点评 本题考查了同底数幂的乘法，利用互为相反数的偶数次幂相等，互为相反数的奇数次幂互为相反数，得出同底数幂的乘法是解题关键．
练习册系列答案
相关题目
如图，将△ABC纸片折叠，使C落在三角形的内部，求证：∠ADC+∠BEC=2∠C．
如图，BE⊥AC、CF⊥AB于点E、F，BE与CF交于点D，AD平分∠BAC，求证：AB=AC．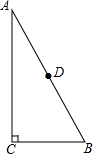
如图，在Rt△ABC中，∠C=90°，D是AB的中点．AC=4，BC=2，以C为圆心，$\sqrt{5}$为半径作⊙C，A，B，D三点与⊙C的位置关系如何．
如图，要设计一本书的封面，封面长25cm，宽15cm．正中央是一个与整个封面长宽比例相同的矩形，如果要使四周边衬所占面积是封面面积的$\frac{9}{25}$，且上、下边衬等宽，左、右边衬等宽，则上下边衬的宽4.5cm．