题目内容
 △ABC中,F是BC中点,D在AC上,
△ABC中,F是BC中点,D在AC上,| AD |
| CD |
| n |
| m |
| OA |
| OF |
考点:平行线分线段成比例
专题:
分析:如图,作辅助线;证明CD=2DE;进而证明
=
;证明
=
,即可解决问题.
| AD |
| DE |
| 2n |
| m |
| OA |
| OF |
| AD |
| DE |
解答: 解:如图,过点F作FE∥BD,交AC于点E;
解:如图,过点F作FE∥BD,交AC于点E;
∵F是BC中点,
∴DE=CE,CD=2DE;
∵
=
,
∴
=
;
∵FE∥BD,
∴
=
,
即
的值为
.
 解:如图,过点F作FE∥BD,交AC于点E;
解:如图,过点F作FE∥BD,交AC于点E;∵F是BC中点,
∴DE=CE,CD=2DE;
∵
| AD |
| CD |
| n |
| m |
∴
| AD |
| DE |
| 2n |
| m |
∵FE∥BD,
∴
| OA |
| OF |
| AD |
| DE |
即
| OA |
| OF |
| 2n |
| m |
点评:该题主要考查了平行线分线段成比例定理及其应用问题;解题的关键是作辅助线;灵活运用平行线分线段成比例定理等几何知识点来分析、解答.

练习册系列答案
相关题目
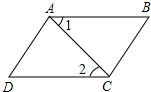 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,下列推理不正确的是( )
如图,下列推理不正确的是( )| A、∵AB∥CD,∴∠ABC+∠C=180° |
| B、∵∠1=∠2,∴AD∥BC |
| C、∵AD∥BC,∴∠3=∠4 |
| D、∵∠A+∠ADC=180°,∴AB∥CD |
设计抽样调查方案时,常用到抽签的方法,抽签中确保样本代表性的关键是( )
| A、制签 | B、搅拌均匀 |
| C、逐一抽取 | D、抽取不放回 |
 如图,一块长方形草地长20,宽15,中间有一条宽为a的拐直角的小路,则草地面积为( )
如图,一块长方形草地长20,宽15,中间有一条宽为a的拐直角的小路,则草地面积为( )| A、20a |
| B、15a |
| C、300 |
| D、(20-a)(15-a) |
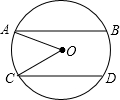 如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.
如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.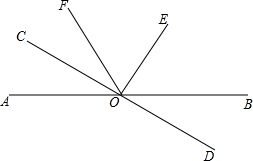 如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.