题目内容
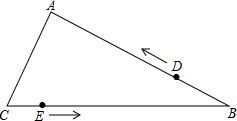 如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值.
如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值.考点:相似三角形的判定
专题:动点型
分析:由于相似三角形的对应边不能确定,故应分△BDE∽△BAC,△BED∽△BAC两种情况进行讨论.
解答:解:∵点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,
∴BD=t,BE=8-2t,
∴△BDE∽△BAC时,
=
,即
=
,解得t=2.4(秒);
当△BED∽△BAC时,
=
,即
=
,解得t=
(秒).
综上所述,t的值为2.4秒或
秒.
∴BD=t,BE=8-2t,
∴△BDE∽△BAC时,
| BD |
| AB |
| BE |
| BC |
| t |
| 6 |
| 8-2t |
| 8 |
当△BED∽△BAC时,
| BD |
| BC |
| BE |
| AB |
| t |
| 8 |
| 8-2t |
| 6 |
| 32 |
| 11 |
综上所述,t的值为2.4秒或
| 32 |
| 11 |
点评:本题考查的是相似三角形的判定,熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
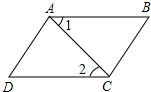 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,下列推理不正确的是( )
如图,下列推理不正确的是( )| A、∵AB∥CD,∴∠ABC+∠C=180° |
| B、∵∠1=∠2,∴AD∥BC |
| C、∵AD∥BC,∴∠3=∠4 |
| D、∵∠A+∠ADC=180°,∴AB∥CD |
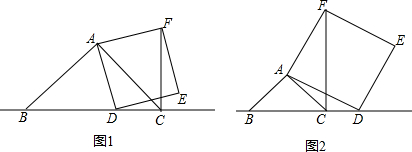
 如图,已知点A、B、C,根据下列语句画图:
如图,已知点A、B、C,根据下列语句画图: