题目内容
4.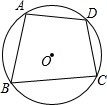 如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.
如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.
分析 首先连接OA,OB,OC,OD,过点O作OE⊥AB于点E,过点O作OF⊥AD于点F,由内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,可得△AOB是顶角为120°的等腰三角形,△AOD是顶角为60°的等腰三角形,△BOC与△COD是等腰直角三角形,继而求得各三角形的面积,从而求得答案.
解答 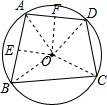 解:连接OA,OB,OC,OD,过点O作OE⊥AB于点E,过点O作OF⊥AD于点F,
解:连接OA,OB,OC,OD,过点O作OE⊥AB于点E,过点O作OF⊥AD于点F,
∵内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,
∴∠AOB=120°,∠BOC=90°,∠AOD=60°,
∴∠COD=90°,
∴∠AOE=60°,∠AOF=30°,
∴OE=$\frac{1}{2}$OA=$\frac{1}{2}$R,AF=$\frac{1}{2}$OA=$\frac{1}{2}$R,
∴AE=$\frac{\sqrt{3}}{2}$R,OF=$\frac{\sqrt{3}}{2}$R,
∴AB=2AE=$\sqrt{3}$R,AD=2AF=R,
∴S△AOB=$\frac{1}{2}$AB•OE=$\frac{1}{2}$×$\sqrt{3}$R×$\frac{1}{2}$R=$\frac{\sqrt{3}}{4}$R2,S△AOD=$\frac{1}{2}$AD•OE=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$R×R=$\frac{\sqrt{3}}{4}$R2,S△BOC=S△COD=$\frac{1}{2}$OB•OC=$\frac{1}{2}$×R×R=$\frac{1}{2}$R2,
∴S四边形ABCD=S△AOB+S△AOD+S△BOC+S△COD=$\frac{\sqrt{3}}{2}$R2+R2.
点评 此题考查了正多边形与圆的知识.注意准确作出辅助线是解此题的关键.

| A. | 132° | B. | 66° | C. | 60° | D. | 48° |
$\sqrt{2}$,$\root{3}{1000}$,π,-3.1416,$\sqrt{9}$,$\frac{1}{3}$,0.030030003…,0.57143,$\root{3}{-1}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
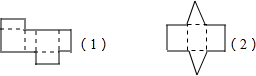 下面是两种立体图形的展开图.请分别写出这两个立体图形的名称:
下面是两种立体图形的展开图.请分别写出这两个立体图形的名称: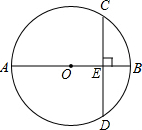 如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.
如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.