题目内容
15.阅读材料,回答问题:材料:为解方程x4-x2-6=0,然后设x2=y,于是原方程可化为y2-y-6=0,解得y1=-2,y2=3.当y=-2时,x2=-2不合题意舍去;当y=3时,x2=3,解得x1=$\sqrt{3}$,x2=-$\sqrt{3}$.故原方程的根为x1=$\sqrt{3}$,x2=-$\sqrt{3}$.请你参照材料给出的解题方法,解下列方程
①(x2-x)2-4(x2-x)-12=0.
②$\frac{2x-1}{x}$-$\frac{3x}{2x-1}$=2.
分析 (1)设y=x2-x,把原方程化为一元二次方程,解方程得到答案;
(2)设$\frac{2x-1}{x}$=y,把原方程化为简单的分式方程,解方程即可.
解答 解:①设y=x2-x,
原方程可化为y2-4y-12=0,
解得y1=-2,y2=6,
当y=-2时,x2-x=-2,
即x2-x+2=0,方程无解,
当y=6时,x2-x=6,
即x2-x-6=0,
解得,x1=-2,x2=3,
故原方程的根为x1=-2,x2=3;
②设$\frac{2x-1}{x}$=y,
原方程可化为y2-2y-3=0,
解得y1=-1,y2=3,
当y=-1时,$\frac{2x-1}{x}$=-1,
解得x=$\frac{1}{3}$,
当y=3时,$\frac{2x-1}{x}$=3,
解得,x=-1,
故原方程的根为x1=$\frac{1}{3}$,x2=-1.
点评 本题考查的是换元法解一元二次方程和分式方程,通过阅读掌握换元法的一般步骤是解题的关键,注意一元二次方程和分式方程的解法.

练习册系列答案
相关题目
6.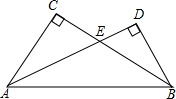 如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
 如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )| A. | ∠CAE>∠DBE | B. | ∠CAE=∠DBE | C. | ∠CAE<∠DBE | D. | 无法确定 |
3.南通2015年金秋港口经贸洽谈会成交额约为2643万元,这一数据用科学记数法表示为( )
| A. | 2.643×103 | B. | 0.2643×108 | C. | 26.43×106 | D. | 2.643×107 |
20.当已知A(-2,y1),B(-1,y2),C(-5,y3)在抛物线y=-$\frac{1}{2}$x2-3x-π上,则y1,y2,y3之间的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2=y3<y1 | D. | y3<y2<y1 |
7.若一个一元二次方程的两根为$\sqrt{2}$+1,$\sqrt{2}$-1,则这个方程是( )
| A. | x2+2$\sqrt{2}$x+1=0 | B. | x2-2$\sqrt{2}$x-1=0 | C. | x2-2$\sqrt{2}$x+1=0 | D. | x2+2$\sqrt{2}$x-1=0 |
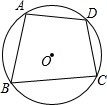 如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.
如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积. 在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)
在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)