题目内容
12.已知线段a=1,b=2,则a,b的比例中项线段长等于$\sqrt{2}$.分析 设线段a,b的比例中项为c,根据比例中项的定义可知,c2=ab,代入数据可直接求得c的值,注意两条线段的比例中项为正数.
解答 解:设线段a,b的比例中项为c,
∵c是长度分别为1、2的两条线段的比例中项,
∴c2=ab=1×2,
即c2=2,
∴c=$\sqrt{2}$(负数舍去).
故答案为:$\sqrt{2}$.
点评 本题主要考查了比例线段.根据比例的性质列方程求解即可.解题的关键是掌握比例中项的定义,如果a:b=b:c,即b2=ac,那么b叫做a与c的比例中项.

练习册系列答案
相关题目
2.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 对称轴x=-1 | B. | 开口向上 | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 函数有最大值,最大值是-2 |
3.南通2015年金秋港口经贸洽谈会成交额约为2643万元,这一数据用科学记数法表示为( )
| A. | 2.643×103 | B. | 0.2643×108 | C. | 26.43×106 | D. | 2.643×107 |
20.当已知A(-2,y1),B(-1,y2),C(-5,y3)在抛物线y=-$\frac{1}{2}$x2-3x-π上,则y1,y2,y3之间的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2=y3<y1 | D. | y3<y2<y1 |
7.若一个一元二次方程的两根为$\sqrt{2}$+1,$\sqrt{2}$-1,则这个方程是( )
| A. | x2+2$\sqrt{2}$x+1=0 | B. | x2-2$\sqrt{2}$x-1=0 | C. | x2-2$\sqrt{2}$x+1=0 | D. | x2+2$\sqrt{2}$x-1=0 |
17.如图所示,画△ABC的一边上的高,下列画法正确的是( )
| A. |  | B. |  | C. |  | D. |  |
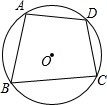 如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.
如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.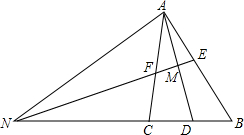 已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N.
已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N.