题目内容
16．已知x1、x2是关于x的一元二次方程x2+（2m+3）x+m2=0的两个不相等的实数根，且满足$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-1，则m的值是（ ）| A． | 3 | B． | 3或-1 | C． | 1 | D． | -3或1 |
分析 根据根与系数关系得出：x1+x2=-2m-3，x1x2=m2，代入$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-1求出m的值，再进行检验即可．
解答 解：∵x1、x2是关于x的一元二次方程x2+（2m+3）x+m2=0的两个不相等的实数根，
∴x1+x2=-2m-3，x1x2=m2，
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-2m-3}{{m}^{2}}$=-1，
解得：m=3，m=-1，
把m=3代入方程得：x2+9x+9=0，△=92-4×1×9＞0，此时方程有解；
把m=-1代入方程得：x2+x+1=0，△=1-4×1×1＜0，此时方程无解，即m=-1舍去．
故选：A．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
6．
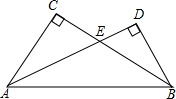如图，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，AD与BC相交于点E，则∠CAE与∠DBE的大小关系是（ ）
如图，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，AD与BC相交于点E，则∠CAE与∠DBE的大小关系是（ ）| A． | ∠CAE＞∠DBE | B． | ∠CAE=∠DBE | C． | ∠CAE＜∠DBE | D． | 无法确定 |
7．若一个一元二次方程的两根为$\sqrt{2}$+1，$\sqrt{2}$-1，则这个方程是（ ）
| A． | x2+2$\sqrt{2}$x+1=0 | B． | x2-2$\sqrt{2}$x-1=0 | C． | x2-2$\sqrt{2}$x+1=0 | D． | x2+2$\sqrt{2}$x-1=0 |
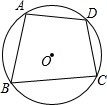如图所示，在半径为R的⊙O中，内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长，求四边形ABCD的面积．
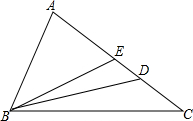如图，D为AC上一点，E为AD一点，且AD=AB，∠EBD=∠DBC．求证：
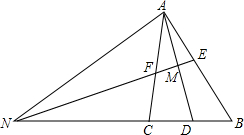已知：AD是Rt△ABC中∠A的平分线，∠C=90°，EF是AD的垂直平分线交AD于M，EF、BC的延长线交于一点N．
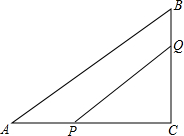如图，△ABC中，∠C=90°，AB=10cm，AC=8cm，点P从A点出发向点C以2cm/s的速度移动，点Q从B点出发向点C以1cm/s的速度移动，当其中一点首先到达终点时运动停止，若P、Q分别同时从A，B出发，几秒后四边形APQB是△ABC面积的$\frac{2}{3}$？
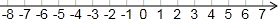在数轴上表示下列各数，并用“＜”号连接．（数轴上表示与“＜”号连接均写原数）