题目内容
13.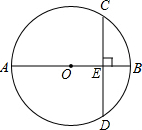 如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.
如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.求:⊙O的半径.
分析 连接OC,设⊙O的半径为Rcm,则OE=(R-4)cm,根据垂径定理求出CE,根据勾股定理得出方程,求出方程的解即可.
解答 解:
连接OC,
设⊙O的半径为Rcm,则OE=(R-4)cm,
∵AB⊥CD,AB为直径,CD=16cm,
∴CE=DE=$\frac{1}{2}$CD=8cm,
在Rt△OEC中,由勾股定理得:OC2=OE2+CE2,
R2=(R-4)2+82,
解得:R=10,
即⊙O的半径为10cm.
点评 本题考查了勾股定理,垂径定理的应用,能根据垂径定理求出CE的长是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.南通2015年金秋港口经贸洽谈会成交额约为2643万元,这一数据用科学记数法表示为( )
| A. | 2.643×103 | B. | 0.2643×108 | C. | 26.43×106 | D. | 2.643×107 |
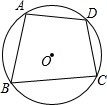 如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.
如图所示,在半径为R的⊙O中,内接四边形ABCD的边AB、BC、AD的长恰好分别等于⊙O内接正三角形、正方形、正六边形的边长,求四边形ABCD的面积.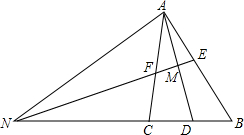 已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N.
已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N.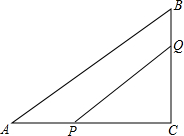 如图,△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从A点出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,当其中一点首先到达终点时运动停止,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的$\frac{2}{3}$?
如图,△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从A点出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,当其中一点首先到达终点时运动停止,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的$\frac{2}{3}$?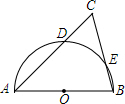 如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为$\sqrt{3}$.
如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为$\sqrt{3}$. 在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)
在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)