题目内容
1.某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图: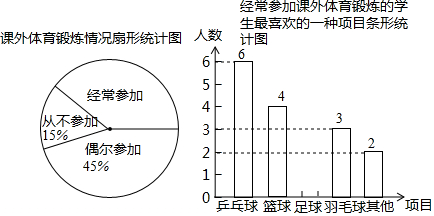
根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为144°;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有1人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率.
分析 (1)用“经常参加”所占的百分比乘以360°计算得到“经常参加”所对应的圆心角的度数;先求出“经常参加”的人数,然后减去其它各组人数得出喜欢足球的人数;进而补全条形图;
(2)用总人数乘以喜欢篮球的学生所占的百分比计算即可得解;
(3)先利用树状图展示所有12种等可能的结果数,找出选中的两个项目恰好是“乒乓球”、“篮球”所占结果数,然后根据概率公式求解.
解答  解:(1)360°×(1-15%-45%)=360°×40%=144°;
解:(1)360°×(1-15%-45%)=360°×40%=144°;
“经常参加”的人数为:40×40%=16人,
喜欢足的学生人数为:16-6-4-3-2=1人;
补全统计图如图所示:
故答案为:144°,1;
(2)全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数约为:1200×$\frac{6}{40}$=180人;
(3)设A代表“乒乓球”、B代表“篮球”、C代表“足球”、D代表“羽毛球”,画树状图如下:
共有12种等可能的结果数,其中选中的两个项目恰好是“乒乓球”、“篮球”的情况占2种,
所以选中“乒乓球”、“篮球”这两个项目的概率是$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.也考查了样本估计总体、扇形统计图和条形统计图.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
12. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )
如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是( )| A. | 以点F为圆心,OE长为半径画弧 | B. | 以点F为圆心,EF长为半径画弧 | ||
| C. | 以点E为圆心,OE长为半径画弧 | D. | 以点E为圆心,EF长为半径画弧 |
10.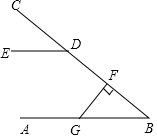 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图,在△ABC中,D、E分别是边AB、AC的中点,则△ADE与△ABC的面积比S△ADE:S△ABC=1:4.
如图,在△ABC中,D、E分别是边AB、AC的中点,则△ADE与△ABC的面积比S△ADE:S△ABC=1:4.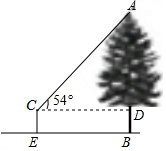 如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为15.3米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)
如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为15.3米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)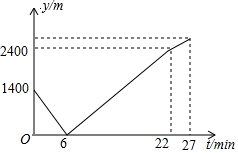 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法: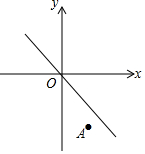 如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).
如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).