题目内容
龙泉地区为促进特种水果的发展,决定对枇杷和水蜜桃的种殖提供政府补贴.该地区某农家乐在改建的10个1亩大小的种植地里分别种植枇杷和水蜜桃(每个种植地只能种一种水果),因资金有限,投入不能超过14万元,并希望获得不低于10.8万元的收益,相关信息如下表所示:(收益=毛利润-成本+政府补贴)
(1)根据以上信息,该农家乐有哪些种殖方案?
(2)请你帮该农家乐设计一种种殖方案,可获得最大收益.
| 种殖种类 | 成本(万元/亩) | 毛利润(万元/亩) | 政府补贴(万元/亩) |
| 枇杷 | 1.5 | 2.5 | 0.2 |
| 水蜜桃 | 1 | 1.8 | 0.1 |
(2)请你帮该农家乐设计一种种殖方案,可获得最大收益.
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)设种植枇杷的面积为x亩,则种植水蜜桃的面积为(10-x)亩,根据条件建立不等式组求出其解即可;
(2)设可获得最大收益为W元,种植枇杷的面积为x亩,则种植水蜜桃的面积为(10-x)亩,根据收益=毛利润-成本+政府补贴建立W与x的函数关系式,由一次函数的性质就可以求出结论.
(2)设可获得最大收益为W元,种植枇杷的面积为x亩,则种植水蜜桃的面积为(10-x)亩,根据收益=毛利润-成本+政府补贴建立W与x的函数关系式,由一次函数的性质就可以求出结论.
解答:解:(1)设种植枇杷的面积为x亩,则种植水蜜桃的面积为(10-x)亩,由题意,得
,
解得:6≤x≤8.
∵x为整数,
∴x=6,7,8.
∴有3种种植方案.
方案1,种植枇杷6亩,水蜜桃4亩;
方案2,种植枇杷7亩,水蜜桃3亩;
方案3,种植枇杷8亩,水蜜桃2亩;
(2)设可获得最大收益为W元,由题意,得
W=(2.5-1.5+0.2)x+(1.8-1+0.1)(10-x),
W=0.3x+9.
∴k=0.3>0,
∴W随x的增大而增大,
∴当x=8时,W最大=11.4万元.
|
解得:6≤x≤8.
∵x为整数,
∴x=6,7,8.
∴有3种种植方案.
方案1,种植枇杷6亩,水蜜桃4亩;
方案2,种植枇杷7亩,水蜜桃3亩;
方案3,种植枇杷8亩,水蜜桃2亩;
(2)设可获得最大收益为W元,由题意,得
W=(2.5-1.5+0.2)x+(1.8-1+0.1)(10-x),
W=0.3x+9.
∴k=0.3>0,
∴W随x的增大而增大,
∴当x=8时,W最大=11.4万元.
点评:本题考查了列一元一次不等式组解实际问题的运用,一元一次不等式组的解法的运用,一次函数的性质的运用,收益=毛利润-成本+政府补贴的关系的运用,方案设计的运用,解答时建立一次函数的关系式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,把一块直角形的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )
如图,把一块直角形的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )| A、65° | B、55° |
| C、60° | D、35° |
 如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,求∠P的度数.
如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,求∠P的度数.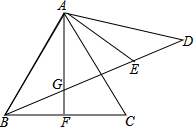 如图,△ABC是等边三角形,F是BC中点,G是AF上任意的一点,D在BG延长线上,且AD=AC,AE平分∠CAD交BD于E.
如图,△ABC是等边三角形,F是BC中点,G是AF上任意的一点,D在BG延长线上,且AD=AC,AE平分∠CAD交BD于E. 已知,如图AD是△ABC的角平分线,DE∥CA交AB于点E,DF∥BA交AC于点F.试问∠1=∠2吗?为什么?
已知,如图AD是△ABC的角平分线,DE∥CA交AB于点E,DF∥BA交AC于点F.试问∠1=∠2吗?为什么?