题目内容

13．已知一个平行四边形的一条对角线将其分为两个全等的等腰直角三角形，且这条对角线长为6cm，则另一条对角线长（　　）cm．
A．6$\sqrt{5}$B．8C．6$\sqrt{5}$或8D．6或6$\sqrt{5}$

分析 利用等腰直角三角形的性质以及正方形的判定方法得出此平行四边形是正方形，即可得出答案．

解答 解：∵一个平行四边形的一条对角线将其分为全等的两个等腰直角三角形，
∴此图形的邻边相等，且对角都是90°，故此平行四边形是正方形，
∵一条对角线的长为6，
∴另一条对角线长为：6．
同理可得出：另外一种情况：这个平行四边形的四个角分别为45°，135°，45°，135°．
此时另外一条对角线的长度为6$\sqrt{5}$．
故另一条对角线长为6或6$\sqrt{5}$．
故选D．

点评 此题主要考查了平行四边形的性质以及等腰直角三角形的性质，得出此平行四边形是正方形是解题关键．

练习册系列答案
相关题目
3．计算：
（1）计算：|1-tan60°|-$\frac{6}{\sqrt{3}}$+（$\sqrt{2}$-1）0
（2）化简：（$\frac{{m}^{2}-1}{{m}^{2}-2m+1}$+$\frac{m}{{m}^{2}-m}$）÷（1+$\frac{2}{m}$）
4．对于正数x，规定f（x）=$\frac{x}{1+x}$，例如f（3）=$\frac{3}{1+3}$=$\frac{3}{4}$，f（$\frac{1}{3}$）=$\frac{\frac{1}{3}}{1+\frac{1}{3}}$=$\frac{1}{4}$，计算f（$\frac{1}{2015}$）+f（$\frac{1}{2014}$）+f（$\frac{1}{2013}$）+…+f（$\frac{1}{3}$）+f（$\frac{1}{2}$）+f（1）+f（2）+f（3）…+f（2013）+f（2014）+f（2015）的结果是（　　）
A．2014B．2014.5C．2015D．2015.5
1．观察下列等式：
1-$\frac{5}{6}$=12×$\frac{1}{6}$   ①
2-$\frac{10}{7}$=22×$\frac{1}{7}$   ②
3-$\frac{15}{8}$=32×$\frac{1}{8}$   ③
…
（1）请写出第四个等式：4-$\frac{20}{9}$=42×$\frac{1}{9}$；
（2）观察上述等式的规律，猜想第n个等式（用含n的式子表示），并证明其正确性．
8．已知：如图，∠1=∠2，∠E=∠F，则AB∥CD吗？说明理由．
18．一条直线y=3x的图象沿x轴向右平移2个单位，所得到的函数关系式是（　　）
A．y=3x+2B．y=3x-2C．y=3x+6D．y=3x-6
5．我们定义一种变换§：对于一个由5个数组成的数列S1，将其中的每个数换成该数在S1中出现的次数，可得到一个新数列S2．例如：当数列S1是 （4，2，3，4，2）时，经过变换§可得到的新数列S2是（2，2，1，2，2）．若数列S1可以由任意5个数组成，则下列的数列可作为S2的是（　　）
A．（1，2，1，2，2）B．（2，2，2，3，3）C．（1，1，2，2，3）D．（1，2，1，1，2）

的运算结果正确的是（　　）

A. B. C. D. a+b
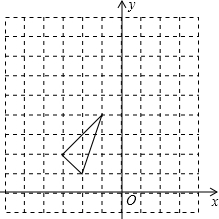20．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，1），B（-1，4），C（-3，2）．
（1）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点坐标；
（2）若点D（a，b）在线段AB上，请直接写出经过（1）的变化后点D的对应点D1坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网