题目内容
11.甲、乙两人分别从相距8千米的两地同时出发,若同向而行,则t1小时后,快者追上慢者,若相向而行,则t2小时后,两人相遇,那么快者速度是慢者速度的( )| A. | $\frac{{t}_{1}}{{t}_{1}+{t}_{2}}$ | B. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}}$ | C. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ | D. | $\frac{{t}_{1}-{t}_{2}}{{t}_{1}+{t}_{2}}$ |
分析 由题意可知:两人同向过程中,在相同的时间中甲比乙多了距离8千米,速度差为$\frac{8}{{t}_{1}}$;在两人相向而行的过程中,速度为两人速度之和为$\frac{8}{{t}_{2}}$,由此求得快者的速度为$\frac{1}{2}$($\frac{8}{{t}_{1}}$+$\frac{8}{{t}_{2}}$),慢者的速度为$\frac{1}{2}$($\frac{8}{{t}_{2}}$-$\frac{8}{{t}_{1}}$),进一步求得答案即可.
解答 解:快者的速度为$\frac{1}{2}$($\frac{8}{{t}_{1}}$+$\frac{8}{{t}_{2}}$)=$\frac{4{t}_{1}+4{t}_{2}}{{t}_{1}{t}_{2}}$,慢者的速度为$\frac{1}{2}$($\frac{8}{{t}_{2}}$-$\frac{8}{{t}_{1}}$)=$\frac{4{t}_{1}-4{t}_{2}}{{t}_{1}{t}_{2}}$,
则快者速度是慢者速度的$\frac{4{t}_{1}+4{t}_{2}}{{t}_{1}{t}_{2}}$÷$\frac{4{t}_{1}-4{t}_{2}}{{t}_{1}{t}_{2}}$=$\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$.
故选:C.
点评 此题考查列代数式,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15.2014年“十一”黄金周期间某品服装原零售价每件200元,凡购买2件以上(含2件),商场推出两种优惠销售方法,第一种:一件按原价,其余按原价的七折优惠;第二种:全部按原价的八折优惠,你在购买相同数量的情况下,要使第一种比第二种方法得到的优惠多,最少需要购买服装( )
| A. | 5件 | B. | 4件 | C. | 3件 | D. | 2件 |
16.下列是方程组$\left\{\begin{array}{l}x+2y=5\\ 2x-y=-5\end{array}$的解的是( )
| A. | $\left\{\begin{array}{l}x=0\\ y=0\end{array}$ | B. | $\left\{\begin{array}{l}x=-5\\ y=0\end{array}$ | C. | $\left\{\begin{array}{l}x=3\\ y=1\end{array}$ | D. | $\left\{\begin{array}{l}x=-1\\ y=3\end{array}$ |
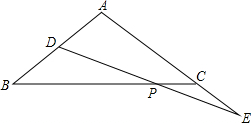 在△ABC中,D在AB上,E在AC的延长线上,连接DE交BC于P,BD=CE,DP=EP,求证:AB=AC.
在△ABC中,D在AB上,E在AC的延长线上,连接DE交BC于P,BD=CE,DP=EP,求证:AB=AC. 如图,?ABCD的周长为20,对角线AC,BD交于点O,OE⊥AC交AD于点E,则△CDE的周长为10.
如图,?ABCD的周长为20,对角线AC,BD交于点O,OE⊥AC交AD于点E,则△CDE的周长为10.