题目内容
1. 如图,?ABCD的周长为20,对角线AC,BD交于点O,OE⊥AC交AD于点E,则△CDE的周长为10.
如图,?ABCD的周长为20,对角线AC,BD交于点O,OE⊥AC交AD于点E,则△CDE的周长为10.
分析 根据平行四边形的性质,得OA=OC,根据线段垂直平分线的性质,得CE=AE,则△DCE的周长是AD+CD的值,即平行四边形的周长的一半.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,AD=BC,CD=AB.
又OE⊥AC,
∴AE=CE.
∴△DCE的周长=CD+DE+CE=CD+AD=$\frac{1}{2}$×20=10,
故答案为:10.
点评 此题考查了平行四边形的性质与线段垂直平分线的性质.此题难度适中,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
相关题目
11.甲、乙两人分别从相距8千米的两地同时出发,若同向而行,则t1小时后,快者追上慢者,若相向而行,则t2小时后,两人相遇,那么快者速度是慢者速度的( )
| A. | $\frac{{t}_{1}}{{t}_{1}+{t}_{2}}$ | B. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}}$ | C. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ | D. | $\frac{{t}_{1}-{t}_{2}}{{t}_{1}+{t}_{2}}$ |
16.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{6}$ | B. | x6÷x3=x2 | C. | $\sqrt{4}$=2 | D. | a2(-a2)=a4 |
6.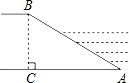 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(| A. | 15m | B. | 20$\sqrt{3}$m | C. | 20m | D. | 10$\sqrt{3}$m |
11.按照如图所示的方法排列黑色小正方形地砖,则第13个图案中黑色小正方形地砖的块数是( )

| A. | 253 | B. | 273 | C. | 293 | D. | 313 |