题目内容
19.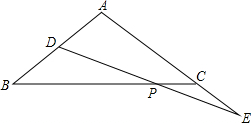 在△ABC中,D在AB上,E在AC的延长线上,连接DE交BC于P,BD=CE,DP=EP,求证:AB=AC.
在△ABC中,D在AB上,E在AC的延长线上,连接DE交BC于P,BD=CE,DP=EP,求证:AB=AC.
分析 利用平行线的性质得出∠GDF=∠CEF进而利用ASA得出△GDF≌△CEP,再利用全等三角形的性质以及等腰三角形的判定得出即可.
解答 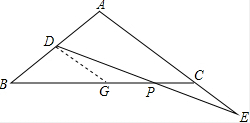 证明:如图过点D作DG∥AE于点G,
证明:如图过点D作DG∥AE于点G,
∵DG∥AC
∴∠GDP=∠CEP(两直线平行,内错角相等),
在△GDP和△CEP中$\left\{\begin{array}{l}{∠GDP=∠CEP}\\{DP=EP}\\{∠DPG=∠CPE}\end{array}\right.$,
∴△GDP≌△CEP(ASA),
∴DG=CE
又∵BD=CE,
∴BD=DG,
∴∠DBG=∠DGB,
∵DG∥AC,
∴∠DGB=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC.
点评 本题考查了全等三角形的判定与性质以及等腰三角形的判定,比较简单,判定两三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”,需要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.甲、乙两人分别从相距8千米的两地同时出发,若同向而行,则t1小时后,快者追上慢者,若相向而行,则t2小时后,两人相遇,那么快者速度是慢者速度的( )
| A. | $\frac{{t}_{1}}{{t}_{1}+{t}_{2}}$ | B. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}}$ | C. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ | D. | $\frac{{t}_{1}-{t}_{2}}{{t}_{1}+{t}_{2}}$ |

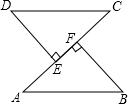 如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.
如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.