题目内容
16.下列是方程组$\left\{\begin{array}{l}x+2y=5\\ 2x-y=-5\end{array}$的解的是( )| A. | $\left\{\begin{array}{l}x=0\\ y=0\end{array}$ | B. | $\left\{\begin{array}{l}x=-5\\ y=0\end{array}$ | C. | $\left\{\begin{array}{l}x=3\\ y=1\end{array}$ | D. | $\left\{\begin{array}{l}x=-1\\ y=3\end{array}$ |
分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x+2y=5①}\\{2x-y=-5②}\end{array}\right.$,
①+②×2得:5x=-5,即x=-1,
把x=-1代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$,
故选D
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.甲、乙两人分别从相距8千米的两地同时出发,若同向而行,则t1小时后,快者追上慢者,若相向而行,则t2小时后,两人相遇,那么快者速度是慢者速度的( )
| A. | $\frac{{t}_{1}}{{t}_{1}+{t}_{2}}$ | B. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}}$ | C. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ | D. | $\frac{{t}_{1}-{t}_{2}}{{t}_{1}+{t}_{2}}$ |
1.已知方程组$\left\{\begin{array}{l}2x+y=-1\\ x+y=0\end{array}\right.$的解是$\left\{\begin{array}{l}x=-1\\ y=1\end{array}\right.$,那么以$\left\{\begin{array}{l}x=-1\\ y=1\end{array}\right.$为解的二元一次方程组有( )
| A. | 有且只有1个 | B. | 有且只有2个 | C. | 不可能有3个 | D. | 有无数个 |
5.在二次函数y=-$\frac{1}{12}$(x-2)2+3的图象上有两点(-1,y1),(1,y2),则y1-y2的值是( )
| A. | 负数 | B. | 零 | C. | 正数 | D. | 不能确定 |
6.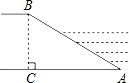 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,则坡面AB的长度是(| A. | 15m | B. | 20$\sqrt{3}$m | C. | 20m | D. | 10$\sqrt{3}$m |
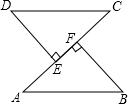 如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.
如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.