题目内容
6.在△ABC中,H是高AD、BE所在直线的交点,且BH=AC,则∠ABC的度数为45°或135°.分析 根据高的可能位置,有2种情况,如图1、图2,通过证明△HBD≌△CAD得AD=BD后求解
解答  解:有2种情况,如图,
解:有2种情况,如图,
∵BH=AC,∠BEC=∠ADC,
∠AHE=∠BHD,∠HAE+∠C=90°,
∠HAE+∠AHE=90°,∴∠C=∠AHE,
∴∠C=∠BHD,
∴△HBD≌△CAD,
∴AD=BD.
如图1时∠ABC=45°;
如图2时∠ABC=135°.
∵HE⊥AC,
∴∠C+∠EBC=90°①,
∵∠HDC=90°,
∴∠H+∠HBD=90°②,
∵∠HBD=∠EBC③,
∴由①②③可得,∠C=∠H,
∵BH=AC,∠ADC=∠BDH,
∠C=∠H,
∴△HBD≌△CAD,
∴AD=BD,
∴∠ABD=45°,
∠ABC=135°;
故答案为:45°或135°
点评 本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.做题时要考虑全面,相等两种情况.

练习册系列答案
相关题目
1.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第7个五边形数是( )
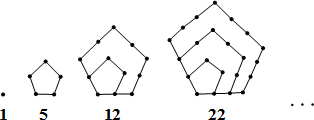

| A. | 62 | B. | 70 | C. | 84 | D. | 108 |
11.甲、乙两人分别从相距8千米的两地同时出发,若同向而行,则t1小时后,快者追上慢者,若相向而行,则t2小时后,两人相遇,那么快者速度是慢者速度的( )
| A. | $\frac{{t}_{1}}{{t}_{1}+{t}_{2}}$ | B. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}}$ | C. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ | D. | $\frac{{t}_{1}-{t}_{2}}{{t}_{1}+{t}_{2}}$ |
15.方程组$\left\{\begin{array}{l}{3x=2y}\\{x+y=50}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=10}\\{y=40}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=15}\\{y=35}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=30}\\{y=20}\end{array}\right.$ |
16.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{6}$ | B. | x6÷x3=x2 | C. | $\sqrt{4}$=2 | D. | a2(-a2)=a4 |

