题目内容
16.在直线y=$\frac{1}{2}$x+1上,且到x轴或y轴距离为2的点的坐标是(2,2)或(-2,0)或(-6,-2).分析 设所求的点P(m,n)根据点P到x轴或y轴距离为2得到|m|=2,|n|=2即可求解.
解答 解:设点P(m,n)到x轴或y轴的距离为2,则|m|=2,|n|=2,所以m=±2,n=±2
当m=2时,n=2,此时点P(2,2),
当m=-2时,n=0,此时点P(-2,0),
当n=2时,m=2,此时点P(2,2),
当n=-2时,m=-6,此时点P(-6,-2).
故答案为:(2,2)或(-2,0)或(-6,-2).
点评 本题考查一次函数的有关性质,点到坐标轴的距离的概念,正确理解概念是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.下列说法正确的是( )
| A. | 若ab=0,则点P(a,b)表示原点 | B. | 坐标轴上的点不属于任何象限 | ||
| C. | 已知点A(3,-2),则它到x轴的距离为3 | D. | 点(1,-a2)在第四象限 |
4.给出下列3个结论:
①边长相等的多边形内角都相等;
②对角线互相垂直的平行四边形是菱形;
③圆心到直线的距离恰好等于圆的半径,则该直线是圆的切线.
其中正确结论的个数有( )
①边长相等的多边形内角都相等;
②对角线互相垂直的平行四边形是菱形;
③圆心到直线的距离恰好等于圆的半径,则该直线是圆的切线.
其中正确结论的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11.一次函数y=-x+4的图象与两坐标轴所围成的三角形的面积为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
1.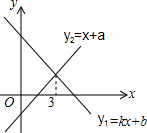 己知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1<y2.正确的个数是( )
己知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1<y2.正确的个数是( )
 己知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1<y2.正确的个数是( )
己知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④x>3时,y1<y2.正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8. 如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
 如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )| A. | -4 | B. | 2 | C. | 4 | D. | 3 |
5.点P在第二象限,且到x轴的距离为5,到y轴的距离为3,则点P的坐标是( )
| A. | (-5,3) | B. | (3,-5) | C. | (-3,5) | D. | (5,-3) |
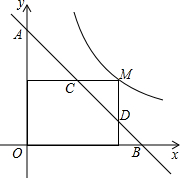 如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.
如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.