题目内容
已知直线L外有两点A、B,AC⊥L,BD⊥L,垂足分别为C、D,且AC=3,BD=8,CD=12.
(1)当A、B在L同侧时,在L上求一点P,使PA+PB值最小,画出图形,并求出最小值.
(2)当A、B在L异侧时,在L上求一点P,使|PA-PB|最大,画出图形,并求出最大值.
(1)当A、B在L同侧时,在L上求一点P,使PA+PB值最小,画出图形,并求出最小值.
(2)当A、B在L异侧时,在L上求一点P,使|PA-PB|最大,画出图形,并求出最大值.
考点:轴对称-最短路线问题
专题:
分析:(1)根据线段垂直平分线的性质,可得B点关于L的对称点B′,根据线段垂直平分线的性质,可得PB=PB′,根据两点之间线段最短,可得答案;
(2)根据线段垂直平分线的性质,可得A点关于L的对称点A′,根据线段垂直平分线的性质,可得PA=PA′根据线段的和差,可得答案.
(2)根据线段垂直平分线的性质,可得A点关于L的对称点A′,根据线段垂直平分线的性质,可得PA=PA′根据线段的和差,可得答案.
解答:解:(1)如图1:
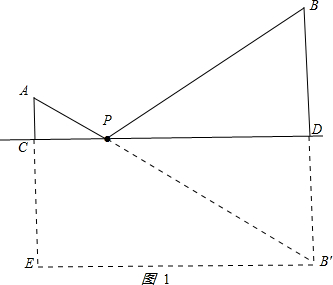
作B点关于l的对称点B′,连接AB′交L于P点,延长AC至E,使B′E⊥AE,
PA+PB最小值=AB′=
=
=
;
(2)如图2:
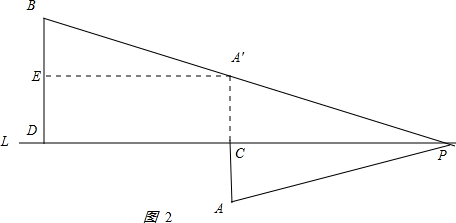 ,
,
作A点关于L的对称点A′,连接BA交L于P点,|PA=PA′,
||PA-PB|最大值=|PA′-PB|=A′B=
=
=13.

作B点关于l的对称点B′,连接AB′交L于P点,延长AC至E,使B′E⊥AE,
PA+PB最小值=AB′=
| AE2+B′E2 |
| 112+122 |
| 265 |
(2)如图2:
 ,
,作A点关于L的对称点A′,连接BA交L于P点,|PA=PA′,
||PA-PB|最大值=|PA′-PB|=A′B=
| BE2+A′E2 |
| 52+122 |
点评:本题考查了轴对称,利用了线段垂直平分线的性质,两点之间线段最短.

练习册系列答案
相关题目
 如图,直线a表示一条公路,点A、B表示两个乡镇,如果要在公路旁(直线a上)修一个车站S,使得AS=BS,请作出点S.
如图,直线a表示一条公路,点A、B表示两个乡镇,如果要在公路旁(直线a上)修一个车站S,使得AS=BS,请作出点S.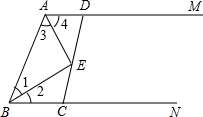 如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,按下列要求画图并回答:画∠MAB、∠NBA的平分线交于E.
如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,按下列要求画图并回答:画∠MAB、∠NBA的平分线交于E.
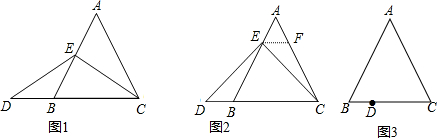
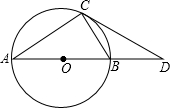 如图,AB是⊙O的直径,D是AB延长线上一点,DC切⊙O于点C,BD=OB.请你根据已知条件和所给图形,写出两个正确结论(除AO=OB=BD外):
如图,AB是⊙O的直径,D是AB延长线上一点,DC切⊙O于点C,BD=OB.请你根据已知条件和所给图形,写出两个正确结论(除AO=OB=BD外):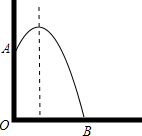 如图,某栋建筑物从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状,如抛物线的函数关系式是y=-
如图,某栋建筑物从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状,如抛物线的函数关系式是y=-