题目内容
(1)如图1,已知点E是等腰梯形ABCD边BC上的点,连接AE交对角线BD于F,在BC上找一点G,连DG交AC于H,使GH=EF(保留作图痕迹,不写做法).
(2)如图2,小明做出图后发现,此时四边形AEGD刚好是等腰梯形,于是小明猜想:如图3在任意梯形ABCD中,AD∥BC,E,F为AB,CD上的点,若EB=FC,∠DAF=∠ADE,则梯形ABCD为等腰梯形.小明猜想正确吗?说明理由.
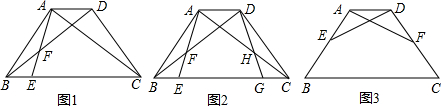
(2)如图2,小明做出图后发现,此时四边形AEGD刚好是等腰梯形,于是小明猜想:如图3在任意梯形ABCD中,AD∥BC,E,F为AB,CD上的点,若EB=FC,∠DAF=∠ADE,则梯形ABCD为等腰梯形.小明猜想正确吗?说明理由.

考点:等腰梯形的性质,等腰梯形的判定
专题:
分析:(1)在BC上截取CG=BE,连接DG与AC相交于H,根据等腰梯形的轴对称性,EF与GH重合;
(2)延长DE、AF分别与BC相交于点G、H,设AF、DE相交于点O,根据等角对等边可得AO=DO,根据两直线平行,内错角相等可得∠OGH=∠OHG,再根据等角对等边可得OG=OH,然后求出AH=DG,再根据对角线相等的梯形是等腰梯形得到四边形AGHD是等腰梯形,然后利用(1)的结论证明即可.
(2)延长DE、AF分别与BC相交于点G、H,设AF、DE相交于点O,根据等角对等边可得AO=DO,根据两直线平行,内错角相等可得∠OGH=∠OHG,再根据等角对等边可得OG=OH,然后求出AH=DG,再根据对角线相等的梯形是等腰梯形得到四边形AGHD是等腰梯形,然后利用(1)的结论证明即可.
解答: 解:(1)GH如图所示;
解:(1)GH如图所示;
(2)根据(1)的作图,由等腰梯形的轴对称性可得AE=DG,
所以,四边形AEGD是等腰梯形,
如图,延长DE、AF分别与BC相交于点G、H,
设AF、DE相交于点O,
∵∠DAF=∠ADE,
∴AO=DO,
∵AD∥BC,
∴∠OGH=∠ADE,∠OHG=∠DAF,
∴∠OGH=∠OHG,
∴OG=OH,
∵AH=AO+OH,DG=DO+OG,
∴AH=DG,
∴四边形AGHD是等腰梯形,
∴梯形ABCD为等腰梯形.
 解:(1)GH如图所示;
解:(1)GH如图所示;(2)根据(1)的作图,由等腰梯形的轴对称性可得AE=DG,
所以,四边形AEGD是等腰梯形,
如图,延长DE、AF分别与BC相交于点G、H,
设AF、DE相交于点O,
∵∠DAF=∠ADE,

∴AO=DO,
∵AD∥BC,
∴∠OGH=∠ADE,∠OHG=∠DAF,
∴∠OGH=∠OHG,
∴OG=OH,
∵AH=AO+OH,DG=DO+OG,
∴AH=DG,
∴四边形AGHD是等腰梯形,
∴梯形ABCD为等腰梯形.
点评:本题考查了梯形的性质,梯形的判定,主要利用了等腰梯形的轴对称性,读懂题目信息,理解(1)的作图理论依据和小明发现问题的方法是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
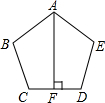 已知,如图,AB=AE,∠BAF=∠EAF,AF⊥CD,且F为CD中点,试说明:BC=ED.
已知,如图,AB=AE,∠BAF=∠EAF,AF⊥CD,且F为CD中点,试说明:BC=ED.