题目内容
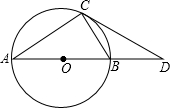 如图,AB是⊙O的直径,D是AB延长线上一点,DC切⊙O于点C,BD=OB.请你根据已知条件和所给图形,写出两个正确结论(除AO=OB=BD外):
如图,AB是⊙O的直径,D是AB延长线上一点,DC切⊙O于点C,BD=OB.请你根据已知条件和所给图形,写出两个正确结论(除AO=OB=BD外):①
②
考点:切线的性质
专题:开放型
分析:CD为切线,所以可以得到角相等和切线与割线的关系;AB是直径,题中的所有半径相等;根据弦切角定理也可得到角相等.
解答:解:∠CDB=∠A,依据是弦切角等于它所夹的弧对的圆周角;
CD2=CB•CA,依据是切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.(答案不唯一,只要符合题意即可)
CD2=CB•CA,依据是切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.(答案不唯一,只要符合题意即可)
点评:此题考查切线的性质,本题为开放型题目,答案不唯一.但选取时一定要根据题中条件按规律选取.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由. 如图,等腰直角三角形ABC经过旋转得到△DBE,∠ACB和∠E都是直角,那么逆时针旋转的角度是
如图,等腰直角三角形ABC经过旋转得到△DBE,∠ACB和∠E都是直角,那么逆时针旋转的角度是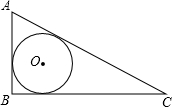 如图,在Rt△ABC中,内切圆⊙O分别与AB、AC、BC相切,且AB=5,AC=13,求内切圆的半径.
如图,在Rt△ABC中,内切圆⊙O分别与AB、AC、BC相切,且AB=5,AC=13,求内切圆的半径.
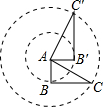 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=2,BC=4,则弧CC′的长为
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=2,BC=4,则弧CC′的长为