题目内容
我们在前面曾遇到过这样一道题目:

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“>”、“<”或“=”)
(2)一般情况,证明结论:如图2,过点E作EF∥BC,交AC于点F. 请你继续完成对以上问题(1)中所填写结论的证明.
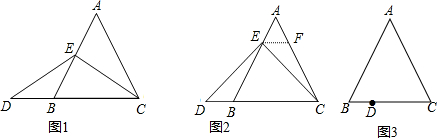
(3)变式探究:如图3,△ABC是等边三角形,D是边BC上一点,点E在BA的延长线上,且BD=AE,此时,CE和DE有何数量关系?请画出图形,作出判断,并说明理由.

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE
(2)一般情况,证明结论:如图2,过点E作EF∥BC,交AC于点F. 请你继续完成对以上问题(1)中所填写结论的证明.

(3)变式探究:如图3,△ABC是等边三角形,D是边BC上一点,点E在BA的延长线上,且BD=AE,此时,CE和DE有何数量关系?请画出图形,作出判断,并说明理由.
考点:全等三角形的判定与性质,等边三角形的性质
专题:探究型
分析:(1)根据等边三角形三线合一的性质可以求得∠DEB=∠D,可证明BD=BE,进一步得到AE=BD;
(2)EF∥BC可得BE=CF,可以证明△CEF≌△DBE,可以求得AE=DB;
(3)过D做DF∥AC,可证△DEF≌△ECA,可以得出CE=DE.
(2)EF∥BC可得BE=CF,可以证明△CEF≌△DBE,可以求得AE=DB;
(3)过D做DF∥AC,可证△DEF≌△ECA,可以得出CE=DE.
解答:解:(1)∵E为等边三角形AB边的中点,
∴∠ECD=30,
∵DE=CE,
∴∠ECD=∠D=30°
∵∠DEB=180°-∠D-∠DBE=30°
∴∠DEB=∠D,
∴BD=BE,
∴AE=BD.
(2)如图2,

∵在等边三角形ABC中,EF∥BC∴BE=CF,
∵DE=CE,
∴∠D=∠ECD
∵∠D+∠DEB=60°,∠ECF+∠ECD=60°,
∴∠ECF=∠DEB
在△CEF和△DBE中,
,
∴△CEF≌△DBE(SAS)
∴AE=DB.
(3)如图3,过D做DF∥AC,则△BDF为等边三角形,∴BD=BF=DF,

∵BD=AE,
∴AB=BF+AF=BD+AF=AE+AF=EF,
∴AC=EF,
∵DF∥AC,
∴∠DFE=∠EAC,
在△DEF和△ECA中,
,
∴△DEF≌△ECA(SAS),
∴CE=DE.
∴∠ECD=30,
∵DE=CE,
∴∠ECD=∠D=30°
∵∠DEB=180°-∠D-∠DBE=30°
∴∠DEB=∠D,
∴BD=BE,
∴AE=BD.
(2)如图2,

∵在等边三角形ABC中,EF∥BC∴BE=CF,
∵DE=CE,
∴∠D=∠ECD
∵∠D+∠DEB=60°,∠ECF+∠ECD=60°,
∴∠ECF=∠DEB
在△CEF和△DBE中,
|
∴△CEF≌△DBE(SAS)
∴AE=DB.
(3)如图3,过D做DF∥AC,则△BDF为等边三角形,∴BD=BF=DF,

∵BD=AE,
∴AB=BF+AF=BD+AF=AE+AF=EF,
∴AC=EF,
∵DF∥AC,
∴∠DFE=∠EAC,
在△DEF和△ECA中,
|
∴△DEF≌△ECA(SAS),
∴CE=DE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中熟练求证三角形全等是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目

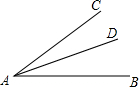 如图,∠BAC=40°,AD平分∠BAC,点P为射线AB上一动点,且△PAD是等腰三角形,则∠APD的度数为
如图,∠BAC=40°,AD平分∠BAC,点P为射线AB上一动点,且△PAD是等腰三角形,则∠APD的度数为 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE=90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由. 如图,等腰直角三角形ABC经过旋转得到△DBE,∠ACB和∠E都是直角,那么逆时针旋转的角度是
如图,等腰直角三角形ABC经过旋转得到△DBE,∠ACB和∠E都是直角,那么逆时针旋转的角度是