题目内容
已知△ABC中,三边a,b,c满足|b-c|+(a-b)2=0,则∠A等于( )
A. 60° B. 45° C. 90° D. 不能确定
 A
【解析】△ABC中,三边a,b,c满足|b-c|+(a-b)2=0∴b-c=0,a-b=0,
∴a=b=c,
∴a=b=c,
∴三角形是等边三角形,
∴∠A=60°.
故选A.
A
【解析】△ABC中,三边a,b,c满足|b-c|+(a-b)2=0∴b-c=0,a-b=0,
∴a=b=c,
∴a=b=c,
∴三角形是等边三角形,
∴∠A=60°.
故选A.
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
如图,E是平行四边形内任一点,若S□ABCD=8,则图中阴影部分的面积是( )
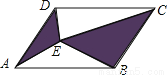
A. 3 B. 4 C. 5 D. 6
 B
【解析】设两个阴影部分三角形的底为AD,CB,高分别为h1,h2,则h1+h2为平行四边形的高,
=4.
所以B选项是正确的.
B
【解析】设两个阴影部分三角形的底为AD,CB,高分别为h1,h2,则h1+h2为平行四边形的高,
=4.
所以B选项是正确的. 化简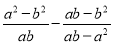 等于( )
等于( )
A. 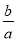 B.
B. 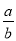 C. ﹣
C. ﹣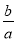 D. ﹣
D. ﹣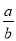
 B
【解析】试题分析:原式=====,故选B.
B
【解析】试题分析:原式=====,故选B. 计算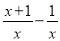 的结果为( )
的结果为( )
A. 1 B. x C. 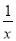 D.
D. 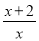
 A
【解析】试题解析:原式
故选A.
A
【解析】试题解析:原式
故选A. 在△ABC中,与∠A相邻的外角是100°,要使△ABC是等腰三角形,则∠B的度是_________.
 80°或50°或20°
【解析】∵∠A的相邻外角是100°,∴∠A=80°.
分两种情况:
(1)当∠A为底角时,另一底角∠B=∠A=80°;
(2)当∠A为顶角时,则底角∠B=∠C= (180°?80°) =50°
(3)当∠B是顶角时,∠B=180°-2∠A=20°.
综上所述,∠B的度数是80°或50°或20°.
80°或50°或20°
【解析】∵∠A的相邻外角是100°,∴∠A=80°.
分两种情况:
(1)当∠A为底角时,另一底角∠B=∠A=80°;
(2)当∠A为顶角时,则底角∠B=∠C= (180°?80°) =50°
(3)当∠B是顶角时,∠B=180°-2∠A=20°.
综上所述,∠B的度数是80°或50°或20°. 在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )
A. 1cm<AB<4cm B. 5cm<AB<10cm
C. 4cm<AB<8cm D. 4cm<AB<10cm
 B
【解析】试题分析:∵在等腰△ABC中,AB=AC,其周长为20cm,∴设AB="AC=x" cm,则BC=(20﹣2x)cm,∴,解得5cm<x<10cm.故选B.
B
【解析】试题分析:∵在等腰△ABC中,AB=AC,其周长为20cm,∴设AB="AC=x" cm,则BC=(20﹣2x)cm,∴,解得5cm<x<10cm.故选B. 已知等腰三角形的两边长分别是3和5,则该三角形的周长是( )
A. 8 B. 9 C. 10或12 D. 11或13
 D
【解析】分两种情况:①当3是腰时,两腰和为6加上底边5,周长为11;②当5是腰时,两腰和为10加上底边3,周长为13.故选D.
D
【解析】分两种情况:①当3是腰时,两腰和为6加上底边5,周长为11;②当5是腰时,两腰和为10加上底边3,周长为13.故选D. 已知:△ABC中,∠B=90°, ∠A、∠C的平分线交于点O,则∠AOC的度数为
A. 60° B. 90° C. 45° D. 135°
 D
【解析】
∵∠B=90°,
∴∠BCA+∠BAC=90°,
∵CD平分∠ACB,AE平分∠CAB,
∴∠OCA=∠BCA,∠OAC=∠BAC,
∴∠OCA+∠OAC=∠BCA+∠BAC=(∠BCA+∠BAC)=45°,
∴∠AOC=135°.
故选D.
D
【解析】
∵∠B=90°,
∴∠BCA+∠BAC=90°,
∵CD平分∠ACB,AE平分∠CAB,
∴∠OCA=∠BCA,∠OAC=∠BAC,
∴∠OCA+∠OAC=∠BCA+∠BAC=(∠BCA+∠BAC)=45°,
∴∠AOC=135°.
故选D. (m-5)2 等于( )
A. m2-5 B. m2-5 2 C. m2-10m+25 D. 25m2-5
 C
【解析】根据完全平方公式可得:(m-5)2 =m2-10m+25 ,故选C.
C
【解析】根据完全平方公式可得:(m-5)2 =m2-10m+25 ,故选C. 
