题目内容
1.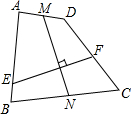 如图,四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,EF⊥MN交AB于点E,交CD于点F.求证:∠AEF=∠DFE.
如图,四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,EF⊥MN交AB于点E,交CD于点F.求证:∠AEF=∠DFE.
分析 连接AC,取AC中点H,连接MH,NH,根据三角形的中位线的性质得到MH∥DC,MH=$\frac{1}{2}$DC,NH∥AB,NH=$\frac{1}{2}$AB,作HG⊥MN 根据平行线的判定和性质即可得到结论.
解答 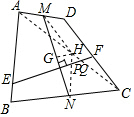 证明:连接AC,取AC中点H,连接MH,NH,
证明:连接AC,取AC中点H,连接MH,NH,
设AC与EF交于Q,HN与EF交于P,
∵M,N为中点,
∴MH∥DC,MH=$\frac{1}{2}$DC,NH∥AB,NH=$\frac{1}{2}$AB,
∵AB=CD,
∴MH=NH,
作HG⊥MN,
∴∠MHG=∠NHG 且EF⊥MN,
∴GH∥EF,
∴∠MHA=∠FCA,∠AHG=∠AQE=∠CQF,∠GHP=∠HPF,
∴∠DFE=∠FCA+∠FQC=∠MHA+∠AHG=∠MHG,
∵NH∥AB,
∴∠AEF=∠HPF,
∴∠MHG=∠GHN=∠HPF=∠AEP=∠DFE,
∴∠AEF=∠DFE.
点评 本题考查了三角形的中位线的性质,平行线的判定和性质,掌握的作出辅助线是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
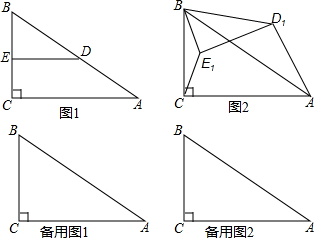
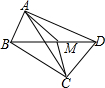 如图,在四边形ABCD中,∠BAD=∠BCD=90°,M是BD的中点,连接AM、CM,那么△MAC是等腰三角形吗?请说明理由.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,M是BD的中点,连接AM、CM,那么△MAC是等腰三角形吗?请说明理由.