题目内容
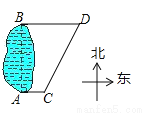
如图，C、D分别是一个湖的南、北两端A和B正东方向的两个村庄，CD=6km，且D位于C的北偏东30°方向上，则AB的长为（ ）
A. 2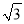
km B. 3
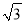km C. 
km 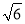D. 3km
B
【解析】试题分析：过点C作CE⊥BD，则∠DCE=30°，根据CD=6km可得：CE=3km，故AB=CE=3km，故选B．
用配方法将y=-2x2+4x+6化成y=a（x+h）2+k的形式，则a+h+k的值为（ ）
A. 5
B. 7
C. -1
D. -2
A
【解析】
∴a=-2，h=-1，k=8
∴a+h+k=-2+（-1）+8=5
故选：A． 用配方法把二次函数y＝l+2x－x2化为y＝a(x－h)2+k的形式，作出它的草图，回答下列问题．
(1)求抛物线的顶点坐标和它与x轴的交点坐标；
(2)当x取何值时，y随x的增大而增大?
(3)当x取何值时，y的值大于0?
y=－(x－1)2＋2(1)顶点坐标为(1，2)，与x轴的两个交点坐标分别为(1－，0)，(1＋，0)(2)当x＜1时，y随x的增大而增大.(3)当l－＜x＜1＋时，y的值大于0
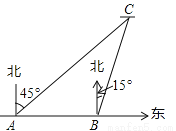
【解析】分析：（1）利用配方法得到y=-(x-1)²+2，则根据二次函数的性质可得到抛物线的顶点坐标；再利用抛物线与x轴的交点问题，通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标；（2）根据二次函数的性质... 如图，有A、B两艘船在大海中航行，B船在A船的正东方向，且两船保持20海里的距离，某一时刻这两艘船同时测得在A的东北方向，B的北偏东15°方向有另一艘船C，那么此时船C与船B的距离是_______海里．（结果保留根号）
20
【解析】试题分析：过点B作BD⊥AC，则△ABD为等腰直角三角形，则BD=10海里，在Rt△CBD中，∠CBD=60°，则BC=2BD=20海里． 海中有一个小岛A，它的周围a海里内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东75°方向上，航行12海里到达D点，这是测得小岛A在北偏东60°方向上．若渔船不改变航线继续向东航行而没有触礁危险，则a的最大值为（ ）
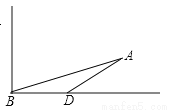
A. 5 B. 6 C. 6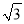
D. 8
B
【解析】试题分析：作AC⊥BD于点C， ∠ABD=90°-75°=15°，
∵∠ADC=90°-60°=30°， ∴∠BAD=∠ADC-∠ABD=30°-15°=15°，
∴∠ABD=∠BAD， ∴BD=AD=12（海里），
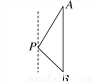
在直角△ADC中，AC=AD=×12=6（海里）．故选B． 如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔60海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为( )
A. 30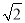
海里 B. 30
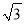海里 C. 60海里 D. 30
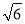海里
A
【解析】试题分析：过点P作PC⊥AB于点C． 在Rt△PAC中，∵PA=60海里，∠PAC=30°， ∴CP=AP=30海里．
在Rt△PBC中，∵PC=30海里，∠PBC=∠BPC=45°， ∴PB=PC=30海里．
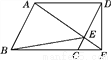
即海轮所在的B处与灯塔P的距离为30海里． 如图，在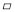
ABCD中，点E在CD边上运动(不与C，D两点重合)，连结AE并延长与BC的延长线交于点F.连结BE，DF，若△BCE的面积为8，则△DEF的面积为________．
8
【解析】试题解析：
故答案为： 如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2．若S=3，则S1+S2的值为（ ）
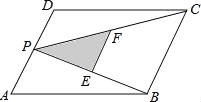
A．24 B．12 C．6 D．3
B
【解析】
试题分析：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，
∴四边形PQCD与四边形APQB都为平行四边形，
∴△PDC≌△CQP，△ABP≌△QPB，
∴S△PDC=S△CQP，S△ABP=S△QPB，
∵EF为△PCB的中位线，
∴EF∥BC，EF=BC，
∴△PEF∽△PBC，且相似比为1：2，
∴S△PEF：S... 公路全长为skm，骑自行车t小时可到达，为了提前半小时到达，骑自行车每小时应多走_____________.
－
【解析】公路全长为skm，骑自行车t小时可到达，则速度为 若提前半小时到达，则速度为 则现在每小时应多走（ ）