题目内容
13.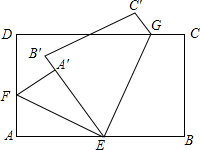 如图,将长方形绒片折叠,折痕为EF和EG,点A落在A处,点B落在B′处,且EA′和EB′重合.
如图,将长方形绒片折叠,折痕为EF和EG,点A落在A处,点B落在B′处,且EA′和EB′重合.(1)∠AEF与∠BEG有何数量关系?请说明理由.
(2)若∠AEF=25°43′,求∠B′EG的补角的大小.
分析 (1)由折叠的性质可得:∠AEF=∠A′EF=$\frac{1}{2}$∠A′EA,∠BEG=∠B′EG=$\frac{1}{2}$∠B′EB,继而可得∠FEG=90°,于是得到结论;
(2)又由被折角∠AEF=25°43′,根据余角的定义即可得到结论.
解答 解:(1)∵由折叠的性质可得:∠AEF=∠A′EF=$\frac{1}{2}$∠A′EA,∠BEG=∠B′EG=$\frac{1}{2}$∠B′EB,
∴∠AEF+∠BEG=$\frac{1}{2}$∠A′EA+$\frac{1}{2}$∠B′EB=$\frac{1}{2}$(∠A′EA+∠B′EB)=90°;
(2)∵∠AEF=25°43′,
∴∠B′EG=90°-25°43′=64°17′.
点评 此题考查了折叠的性质以及角的计算.此题比较简单,注意掌握折叠前后图形的对应关系.

练习册系列答案
相关题目

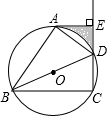 如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.
如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE. 已知抛物线y=ax2-2ax-3a(a<0).
已知抛物线y=ax2-2ax-3a(a<0). 如图所示,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠BEF,FG平分∠EFD,EG⊥FG吗?为什么?
如图所示,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠BEF,FG平分∠EFD,EG⊥FG吗?为什么?