题目内容
14.已知a>0,b>0,且a-5$\sqrt{ab}+6b=0$,求$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}$的值.分析 先因式分解求出$\sqrt{a}$与$\sqrt{b}$之间的关系,然后分别代入计算即可.
解答 解:∵a>0,b>0,且a-5$\sqrt{ab}+6b=0$,
∴($\sqrt{a}$-2$\sqrt{b}$)($\sqrt{a}$-3$\sqrt{b}$)=0,
∴$\sqrt{a}$=2$\sqrt{b}$或$\sqrt{a}$=3$\sqrt{b}$,
①当$\sqrt{a}$=2$\sqrt{b}$时,原式=$\frac{2\sqrt{b}-\sqrt{b}}{2\sqrt{b}+\sqrt{b}}$=$\frac{1}{3}$.
②当$\sqrt{a}$=3$\sqrt{b}$时,原式=$\frac{3\sqrt{b}-\sqrt{b}}{3\sqrt{b}+\sqrt{b}}$=$\frac{1}{2}$.
综上:$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}$的值为$\frac{1}{2}$或$\frac{1}{3}$.
点评 本题考查二次根式的化简求值,灵活掌握因式分解是解题的关键,学会应用已知条件,把已知条件转化为有用的式子,属于中考常考题型.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
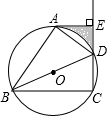 如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.
如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE. 如图所示,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠BEF,FG平分∠EFD,EG⊥FG吗?为什么?
如图所示,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠BEF,FG平分∠EFD,EG⊥FG吗?为什么? 如图,直线a、b被c所截,∠1-∠2=11°,∠3+∠4=169°,求∠1和∠2的度数.[方法提示:注意邻补角].
如图,直线a、b被c所截,∠1-∠2=11°,∠3+∠4=169°,求∠1和∠2的度数.[方法提示:注意邻补角]. 如图,直线AB、CD被直线EF所截.
如图,直线AB、CD被直线EF所截.