题目内容
12.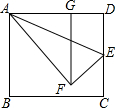 在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为点G,如图,如果AD=3GD,那么DE=3$\sqrt{5}$.
在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为点G,如图,如果AD=3GD,那么DE=3$\sqrt{5}$.
分析 作EH⊥FG于H,如图,设DE=x,先根据折叠的性质得AF=AD=15,EF=DE=x,再利用AD=3GD可计算出DG=5,AG=10,则在Rt△AFG中,根据勾股定理可计算出FG=5$\sqrt{5}$,接着利用四边形DEHG为矩形得到HG=DE=x,HE=GD=5,所以HF=FG-HG=5$\sqrt{5}$-x,然后在Rt△FHE中利用勾股定理得到52+(5$\sqrt{5}$-x)2=x2,然后解方程求出x即可.
解答 解:作EH⊥FG于H,如图, 设DE=x,
设DE=x,
∵△ADE沿直线AE翻折后点D落到点F,
∴AF=AD=15,EF=DE=x,
∵AD=3GD,
∴DG=5,
∴AG=10,
在Rt△AFG中,FG=$\sqrt{A{F}^{2}-A{G}^{2}}$=$\sqrt{1{5}^{2}-1{0}^{2}}$=5$\sqrt{5}$,
易得四边形DEHG为矩形,
∴HG=DE=x,HE=GD=5,
∴HF=FG-HG=5$\sqrt{5}$-x,
在Rt△FHE中,∵HE2+HF2=EF2,
∴52+(5$\sqrt{5}$-x)2=x2,解得x=3$\sqrt{5}$,
即DE=3$\sqrt{5}$.
故答案为3$\sqrt{5}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
3.有六根细木条,它们的长度分别为3、8、12、15、17、18(单位:cm),从中取出三根首尾顺次连结搭成一个直角三角形,则这三根细木条的长度分别为( )
| A. | 3,8,12 | B. | 8,15,17 | C. | 12,15,18 | D. | 3,17,18 |
20.为了了解某市七年级学生的体重情况,相关人员抽查了该市1000名七年级学生,则下列说法中错误的是( )
| A. | 该市七年级学生的全体是总体 | |
| B. | 每个七年级学生的体重是个体 | |
| C. | 抽查的1000名学生的体重是总体的一个样本 | |
| D. | 这次调查样本的容量是1000 |
4.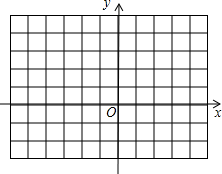 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
(1)填空:a=-3,b=3,c=4;
(2)画出三角形ABC和三角形A′B′C′.
 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:| 三角形ABC | A(a,2) | B(-5,1) | C(-2,0) |
| 三角形A′B′C′ | A′(3,4) | B′(1,b) | C′(c,2) |
(2)画出三角形ABC和三角形A′B′C′.
2.下列化简正确的是( )
| A. | $\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{3}$ | B. | $\sqrt{40}$=5$\sqrt{8}$ | C. | $\sqrt{\frac{8}{9}}$=$\frac{4\sqrt{2}}{3}$ | D. | 8$\sqrt{\frac{3}{2}}$=4$\sqrt{6}$ |
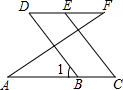 如图,已知∠A=∠F,∠C=∠D,按图填空,括号内注明理由
如图,已知∠A=∠F,∠C=∠D,按图填空,括号内注明理由